Gostaria que aguem me ajudasse nesta questão:
1) Sendo O a origem de um sistema de coordenadas, e dado o ponto A = (6, 8), encontre as coordenadas do ponto B tal que o segmento OB tem comprimento 4 é perpendicular ao segmento OA no ponto O. DICA: Use que tg(90+?)=(sen(90+?))/(cos(90+?)).
Eu ja fiz o gráfico no geogebra sei o resultado mas não sei como fazer para chegar no mesmo.
Obrigada .
as coordenadas do ponto B. O comprimento do segmento 
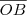é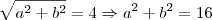 
. 
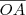, temos que seu coeficiente angular é 
. Sabemos também que 
. Agora basta resolver o sistema com as duas equações e você chegará em duas respostas. 
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png "\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}")
![\sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png "\sqrt[]{2}")
e elevar ao quadrado os dois lados)