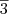 na sua franção geratriz?
na sua franção geratriz?Eu sei que a resposta é
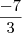 só não sei como transformá-la.
só não sei como transformá-la.
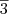 na sua franção geratriz?
na sua franção geratriz?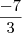 só não sei como transformá-la.
só não sei como transformá-la.
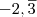
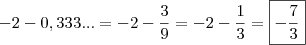

 nem
nem 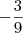


 . Faça na calculadora 3 dividido por 9 e veja que vai aparecer 0,333... [ou clique aqui].
. Faça na calculadora 3 dividido por 9 e veja que vai aparecer 0,333... [ou clique aqui].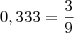 . Substituindo naquele repartição que ele tinha feito:
. Substituindo naquele repartição que ele tinha feito:

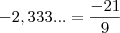
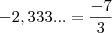


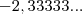 certo.
certo. tudo certo até aqui?
tudo certo até aqui?
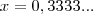
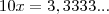
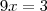
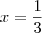 como queríamos encontrar,desta forma encontramos,
como queríamos encontrar,desta forma encontramos,


GABRUEL escreveu:x=0,3333...
10x=3,3333...
Subtraindo temos,
9x=3
Como assim 9x? da onde surgiu?

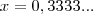 significa que temos "infinitos" números 3, certo?
significa que temos "infinitos" números 3, certo?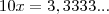 e mesmo assim continuaremos tendo "infinitos" números 3.
e mesmo assim continuaremos tendo "infinitos" números 3.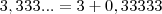 certo? Apenas separei a parte inteira da parte fracionária.
certo? Apenas separei a parte inteira da parte fracionária.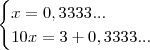
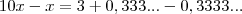
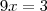

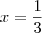


Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes

 .
.
 :
: