 por nietzsche » Dom Jan 16, 2011 16:10
por nietzsche » Dom Jan 16, 2011 16:10
Boa tarde.
Seja Gn = {x é real: -1/n < x < 1+1/n } , onde n é natural.
A interseção dos conjuntos Gn é o conjunto F = {x é real: 0<= x <= 1}.
Se x pertence a interseção dos Gn, então ele pertence a todos Gn, para todo n. Mas como explicar que o 0 e o 1 sãos as cotas que limitam o intervalo de F?
Agradeço desde já.
-
nietzsche
- Usuário Parceiro

-
- Mensagens: 99
- Registrado em: Qua Jan 12, 2011 14:09
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por nietzsche » Sex Jun 24, 2011 22:33
por nietzsche » Sex Jun 24, 2011 22:33
nietzsche escreveu:Boa tarde.
Seja Gn = {x é real: -1/n < x < 1+1/n } , onde n é natural.
A interseção dos conjuntos Gn é o conjunto F = {x é real: 0<= x <= 1}.
Se x pertence a interseção dos Gn, então ele pertence a todos Gn, para todo n. Mas como explicar que o 0 e o 1 sãos as cotas que limitam o intervalo de F?
Agradeço desde já.
-
nietzsche
- Usuário Parceiro

-
- Mensagens: 99
- Registrado em: Qua Jan 12, 2011 14:09
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por MarceloFantini » Sáb Jun 25, 2011 01:33
por MarceloFantini » Sáb Jun 25, 2011 01:33
Bom, temos que

. O que nós queremos é determinar F tal que

. Eu pensei assim: se você tomar o limite dos dois lados da desigualdade, com

, veja que o único conjunto que pertence a todos é realmente
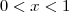
, pois

. Isto é mais uma idéia intuitiva, não considero isso como um argumento rigoroso.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por nietzsche » Sáb Jun 25, 2011 11:09
por nietzsche » Sáb Jun 25, 2011 11:09
olá marcelo fantini,
eu pensei nisso que vc disse. mas minha dúvida é porque depois do limite o intervalo em que x está fica fechado: 0<= x <= 1?
esse exemplo é do livro 'elements of real analysis', do autor bartle, ou seja, é verdade que x pertence a [0,1]. por que não somente ]0,1[ ?
toda idéia é bem-vinda.
abraço.
-
nietzsche
- Usuário Parceiro

-
- Mensagens: 99
- Registrado em: Qua Jan 12, 2011 14:09
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por MarceloFantini » Sáb Jun 25, 2011 11:15
por MarceloFantini » Sáb Jun 25, 2011 11:15
Não sei se há razão específica, afinal de contas
![]0,1[ \subset [0,1] ]0,1[ \subset [0,1]](/latexrender/pictures/7ad02b7ee807696544aad5b57470d4ba.png)
. Talvez para ficar mais elegante.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por nietzsche » Sáb Jun 25, 2011 13:44
por nietzsche » Sáb Jun 25, 2011 13:44
creio que não seja pra ficar mais elegante. se trabalharmos com derivadas, por exemplo, nesse intervalo, os extremos serão muito importantes. então vcai importar se estamos num intervalo aberto ou fechado.
vale a pena estudar para descobrir a resposta. carrego essa dúvida desde o primeiro semestre e ainda não sei como resolvê-la. não sei se é óbvia a resposta, considerando a teoria de conjuntos, mas ainda não vi a resposta dessa questão.
-
nietzsche
- Usuário Parceiro

-
- Mensagens: 99
- Registrado em: Qua Jan 12, 2011 14:09
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por nietzsche » Sáb Jun 25, 2011 13:46
por nietzsche » Sáb Jun 25, 2011 13:46
pensei em algo agora: talvez saia por indução. depois vou tentar fazer.
-
nietzsche
- Usuário Parceiro

-
- Mensagens: 99
- Registrado em: Qua Jan 12, 2011 14:09
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por MarceloFantini » Dom Jun 26, 2011 01:07
por MarceloFantini » Dom Jun 26, 2011 01:07
Em termos de derivada basta o intervalo ser aberto, não?
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por nietzsche » Dom Jun 26, 2011 01:18
por nietzsche » Dom Jun 26, 2011 01:18
o que quis dizer é que a se união de infinitos conjuntos Gn, for um conjunto aberto e vc fechar e for tentar resolver um problema de equações diferenciais (por exemplo o problema de sturm-liouville, onde os extremos do intervalo são importante), vc está resolvendo um outro problema. e se a função não tá definida, se os limites laterais não existirem? vai surgir problemas. por isso que falei que "acochambrar" um intervalo (a,b) para um [a,b] não á algo trivial se estamos lidando com derivadas.
-
nietzsche
- Usuário Parceiro

-
- Mensagens: 99
- Registrado em: Qua Jan 12, 2011 14:09
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por MarceloFantini » Dom Jun 26, 2011 01:21
por MarceloFantini » Dom Jun 26, 2011 01:21
Porque não pergunta a algum de seus professores?
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por nietzsche » Dom Jun 26, 2011 20:30
por nietzsche » Dom Jun 26, 2011 20:30
por que todos do fórum não perguntam a seus professores???? assim não precisaria dum fórum.
-
nietzsche
- Usuário Parceiro

-
- Mensagens: 99
- Registrado em: Qua Jan 12, 2011 14:09
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por MarceloFantini » Dom Jun 26, 2011 20:38
por MarceloFantini » Dom Jun 26, 2011 20:38
Assim como fiz no outro post, quero deixar claro que não tenho intenção de te ofender, portanto peço desculpas se o comentário que fiz soou ofensivo. Fiz o questionamento pois parece-me que é uma dúvida que permanece a muito tempo (desde o primeiro semestre da graduação, segundo você) e que portanto parece razoável que se no fórum não surgiram respostas, seria natural perguntar a alguém na faculdade sobre um esclarecimento na questão.
Por curiosidade, qual semestre da gradução você está? Abraços.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por nietzsche » Dom Jun 26, 2011 21:26
por nietzsche » Dom Jun 26, 2011 21:26
estou no penúltimo semestre, tirando os atrasos. essa dúvida surgiu quando li o livro do bartle, depois de já ter feito um primeiro curso de análise. mas como não precisei resolver, não fui atrás. geralmente essa parte de teoria de conjuntos, é dado com maior enfoque em outras discplinas mais avançadas, visto que é bem confuso falar de uma sequência de conjuntos, intervalos, etc, sem termos uma noção básica de topologia da reta, limites, entre outros assuntos. queria ver até onde minha dúvida vai, até que ponto eu precisaria aprender matemática para resolve-la de forma completa, por isso não quis procurar um professor. é bom rever coisas passadas, com uma nova visão.
tinha soado meu agressivo, mas vi que não foi nada de mais. estamos aqui pra aprender, discutir, descobrir coisas, então é bom deixar de lado qualquer tipo de agressão.
um abraço
-
nietzsche
- Usuário Parceiro

-
- Mensagens: 99
- Registrado em: Qua Jan 12, 2011 14:09
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
Voltar para Conjuntos
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Interseção de conjuntos
por Lana Brasil » Sáb Fev 15, 2014 14:23
- 2 Respostas
- 1662 Exibições
- Última mensagem por ralenon

Ter Mar 18, 2014 14:43
Conjuntos
-
- União/Interseção de Conjuntos
por joaofonseca » Qui Jan 10, 2013 00:28
- 1 Respostas
- 2607 Exibições
- Última mensagem por fraol

Seg Fev 11, 2013 17:41
Conjuntos
-
- Interseção de bissetrizes
por Roni Martins » Ter Fev 16, 2010 13:22
- 3 Respostas
- 4845 Exibições
- Última mensagem por Douglasm

Ter Fev 16, 2010 15:15
Geometria Plana
-
- Interseção das retas
por Julia Capistrano » Seg Fev 28, 2011 20:49
- 4 Respostas
- 3950 Exibições
- Última mensagem por Julia Capistrano

Ter Mar 01, 2011 23:36
Geometria Plana
-
- conjunto interseção
por aline lima » Seg Ago 15, 2011 14:18
- 1 Respostas
- 2187 Exibições
- Última mensagem por Molina

Ter Ago 16, 2011 15:17
Conjuntos
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
(FGV) ... função novamente rs
Autor:
my2009 - Qua Dez 08, 2010 21:48
Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
Assunto:
(FGV) ... função novamente rs
Autor: Anonymous - Qui Dez 09, 2010 17:25
Uma função de 1º grau é dada por

.
Temos que para

,

e para

,

.

Ache o valor de

e

, monte a função e substitua

por

.
Assunto:
(FGV) ... função novamente rs
Autor:
Pinho - Qui Dez 16, 2010 13:57
my2009 escreveu:Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
f(x)= 2.x
f(3)=2.3=6
f(4)=2.4=8
f(10)=2.10=20
Assunto:
(FGV) ... função novamente rs
Autor:
dagoth - Sex Dez 17, 2010 11:55
isso ai foi uma questao da FGV?
haahua to precisando trocar de faculdade.
Assunto:
(FGV) ... função novamente rs
Autor:
Thiago 86 - Qua Mar 06, 2013 23:11
Saudações!

ví suaquestão e tentei resolver, depois você conta-me se eu acertei.
Uma função de 1º grau é dada por y=3a+b
Resposta :
3a+b=6 x(4)
4a+b=8 x(-3)
12a+4b=24
-12a-3b=-24
b=0
substituindo b na 1°, ttenho que: 3a+b=6
3a+0=6
a=2
substituindo em: y=3a+b
y=30+0
y=30

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.




 . O que nós queremos é determinar F tal que
. O que nós queremos é determinar F tal que  . Eu pensei assim: se você tomar o limite dos dois lados da desigualdade, com
. Eu pensei assim: se você tomar o limite dos dois lados da desigualdade, com  , veja que o único conjunto que pertence a todos é realmente
, veja que o único conjunto que pertence a todos é realmente 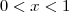 , pois
, pois  . Isto é mais uma idéia intuitiva, não considero isso como um argumento rigoroso.
. Isto é mais uma idéia intuitiva, não considero isso como um argumento rigoroso.


![]0,1[ \subset [0,1] ]0,1[ \subset [0,1]](/latexrender/pictures/7ad02b7ee807696544aad5b57470d4ba.png) . Talvez para ficar mais elegante.
. Talvez para ficar mais elegante.











 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.
