Verificar se os pontos A(5, – 5, 6) e B(4, – 1, 12) pertencem a reta
s:
=
=
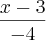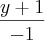R.Transformei de simetrica p/ parametrica:
t=
x=-3-4yt=
y=1-tt=
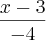
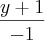
z=-2-5tPara A(5,-5,6)
x=3-4t 5=3-4t
y=1-t -5=1-t
z=-2-5t 6=-2-5t
t=6
A pertence a s
Para B(4,-1,12)
x=3-4t 4=3-4t
y=1-t -1=1-t
z=-2-5t 12=-2-5t
t=2
B não pertence a s
Desde já agradeço
.
por ![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png "{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}")
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png "{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}")
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio. ![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png "{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}")
da seguinte forma:
.
da seguinte forma:
.