 por Aliocha Karamazov » Sáb Jun 18, 2011 22:36
por Aliocha Karamazov » Sáb Jun 18, 2011 22:36
Galera, essa questão é bem óbvia, mas eu preciso provar. Está numa lista que trata do princípio da indução finita. Não consegui encontrar uma maneira para provar isso, apesar de ser evidente que é verdade. Esse é o enunciado:
Prove que um caixa eletrônico pode entregar ao usuário qualquer valor maior ou igual a R$4 usando apenas notas de dois e de cinco reais.
Agradeço a quem puder me ajudar.
-
Aliocha Karamazov
- Usuário Parceiro

-
- Mensagens: 90
- Registrado em: Qua Mar 16, 2011 17:26
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Física
- Andamento: cursando
 por Neperiano » Ter Jun 21, 2011 16:17
por Neperiano » Ter Jun 21, 2011 16:17
Ola
Não sei como se prova, mas tenta mostrar que usando 2 e 5 dá para entregar valores maior ou igual a 4
Tipo:
2 + 2 = 4
2 + 2 + 2 = 6
em geral
2^n+1 sempre vai da maior que um para n maior ou igual a 1
5 = 5
5 + 5 = 10
5^n para n maior que 0
5+ 2 = 7
2 + 2 + 5 = 9
Como disse não sei como se prova, mas de voce souber é so demostrar
Atenciosamente
Sómente os mortos conhecem o fim da guerra
"Platão"
-

Neperiano
- Colaborador Voluntário

-
- Mensagens: 960
- Registrado em: Seg Jun 16, 2008 17:09
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia de Produção
- Andamento: cursando
 por Molina » Ter Jun 21, 2011 18:02
por Molina » Ter Jun 21, 2011 18:02
Boa tarde.
Pensei em provar que todo número N maior ou igual a 4 podem ser escritos da forma

.
Separar os casos em pares e ímpares seria a continuação deste demonstração.
Acho que segue por aí...
Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por MarceloFantini » Ter Jun 21, 2011 21:00
por MarceloFantini » Ter Jun 21, 2011 21:00
Note que a sua expressão é inválida, Neperiano. Os valores de
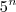
e
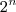
não cobrem alguns valores possíveis.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por Molina » Qua Jun 22, 2011 00:11
por Molina » Qua Jun 22, 2011 00:11
Boa noite.
Achei um padrão de escrever todos os números pares e ímpares maiores ou iguais a 4.
Os valores pares não precisam de notas de 5 reais, apenas de notas de 2 reais:
4 = 2*2
6 = 2*3
8 = 2*4
10 = 2*5
12 = 2*6
N = 2*k, onde k é a quantidade de notas de 2 reais necessárias para formar o valor N
Os valores ímpares precisam apenas de UMA nota de 5 reais e ALGUMAS notas de 2 reais:
5 = 2*0 + 5*1
7 = 2*1 + 5*1
9 = 2*2 + 5*1
11 = 2*3 + 5*1
13 = 2*4 + 5*1
N = 2*k + 5, onde k é a quantidade de notas de 2 reais necessárias para formar o valor N
Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
Voltar para Sequências
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- O custo da caixa hexagonal
por maria cleide » Seg Out 24, 2011 22:17
- 1 Respostas
- 1352 Exibições
- Última mensagem por Neperiano

Ter Out 25, 2011 15:51
Geometria Plana
-
- Volume de uma caixa retangular
 por Andreza » Sáb Nov 12, 2011 10:02
por Andreza » Sáb Nov 12, 2011 10:02
- 1 Respostas
- 1772 Exibições
- Última mensagem por LuizAquino

Qui Nov 17, 2011 22:16
Geometria Espacial
-
- Construir fluxo de caixa
por Mariana Feijo » Seg Nov 26, 2012 22:41
- 1 Respostas
- 2752 Exibições
- Última mensagem por MarceloFantini

Ter Nov 27, 2012 00:49
Matemática Financeira
-
- Fluxo de Caixa - Solução
por goon » Ter Jul 09, 2013 11:45
- 0 Respostas
- 1244 Exibições
- Última mensagem por goon

Ter Jul 09, 2013 11:45
Matemática Financeira
-
- Rendas Certas (Fluxo de Caixa)
por Danilo Dias Vilela » Qua Mar 31, 2010 19:57
- 1 Respostas
- 2475 Exibições
- Última mensagem por Neperiano

Qua Mar 31, 2010 21:17
Matemática Financeira
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



 .
.
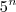 e
e 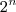 não cobrem alguns valores possíveis.
não cobrem alguns valores possíveis.
 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.