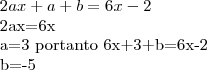por Fabricio dalla » Sex Jun 17, 2011 14:28
por Fabricio dalla » Sex Jun 17, 2011 14:28
na funçao f:R--->R tem-se uma parabola da funçao f(x+1)-f(x)=6x-2 entao o menor valor de f(x) é ?
obs:é eu pensava que ja vi de tudo de funçao de segundo grau.ficarei muito grato quem resolver!
-
Fabricio dalla
- Colaborador Voluntário

-
- Mensagens: 111
- Registrado em: Sáb Fev 26, 2011 17:50
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por LuizAquino » Dom Jun 19, 2011 12:40
por LuizAquino » Dom Jun 19, 2011 12:40
O texto está muito mal escrito.
Não seria algo como segue abaixo?
A função f:R--->R tem como gráfico uma parábola. Se f é tal que f(x + 1) - f(x) = 6x - 2, então o menor valor de f(x) é?Considerando que esse é o texto, primeiro lembre-se que f terá o formato f(x) = ax² + bx + c.
Agora, determine o polinômio f(x+1) - f(x) e compare os seus coeficientes com os do polinômio 6x - 2. Com isso você verá que pode determinar os coeficientes a e b. Note que apenas com os dados desse exercício não temos como determinar o coeficiente c.
O menor valor de f(x) será
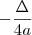
. Esse valor ficará em função do coeficiente c.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por Fabricio dalla » Dom Jun 19, 2011 15:53
por Fabricio dalla » Dom Jun 19, 2011 15:53
na verdade eu que errei(desculpa) pois ele pergunta o menor valor de x para f(x) se menor ai meu amigo explicou
![f(x+1)-f(x)=6x-2
[tex]
a{(x+1)}^{2}+b(x+1)+c-a{x}^{2}-bx-c=6x-2 f(x+1)-f(x)=6x-2
[tex]
a{(x+1)}^{2}+b(x+1)+c-a{x}^{2}-bx-c=6x-2](/latexrender/pictures/abb3718cb039122094dcb3d793ac73ae.png)
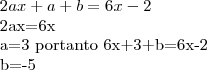
corrigindo o que tinha escrevido pois ele pergunta o xVe nao Yv temos que xV=5/6 a resposta.
desculpe por fazer vc perder tempo no meu erro de digitaçao LuizAquino. vlws pela atençao!
-
Fabricio dalla
- Colaborador Voluntário

-
- Mensagens: 111
- Registrado em: Sáb Fev 26, 2011 17:50
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
Voltar para Funções
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Função do segundo grau
por gustavoluiss » Dom Nov 28, 2010 17:27
- 7 Respostas
- 5531 Exibições
- Última mensagem por alexandre32100

Qua Dez 01, 2010 15:39
Álgebra Elementar
-
- Equação do segundo grau
por VtinxD » Qui Jan 27, 2011 23:03
- 1 Respostas
- 3894 Exibições
- Última mensagem por douglaspezzin

Dom Jun 19, 2011 09:55
Desafios Médios
-
- Inequação do segundo grau
por Aliocha Karamazov » Ter Abr 05, 2011 21:42
- 4 Respostas
- 4687 Exibições
- Última mensagem por Aliocha Karamazov

Qua Abr 06, 2011 18:51
Funções
-
- Inequação de segundo grau
por Aliocha Karamazov » Ter Abr 12, 2011 18:22
- 1 Respostas
- 1487 Exibições
- Última mensagem por FilipeCaceres

Ter Abr 12, 2011 19:53
Funções
-
- Problema do segundo grau
por Alessandra Cezario » Seg Mai 02, 2011 16:52
- 1 Respostas
- 3056 Exibições
- Última mensagem por TheoFerraz

Seg Mai 02, 2011 17:29
Problemas do Cotidiano
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
função demanda
Autor:
ssousa3 - Dom Abr 03, 2011 20:55
alguém poderia me ajudar nesse exercício aqui Uma loja de CDs adquire cada unidade por R$20,00 e a revende por R$30,00. Nestas condições,
a quantidade mensal que consegue vender é 500 unidades. O proprietário estima que, reduzindo o preço para R$28,00, conseguirá vender 600 unidades por mês.
a) Obtenha a função demanda, supondo ser linear
Eu faço ensino médio mas compro apostilas de concursos para me preparar para mercado de trabalho e estudar sozinho não é fácil. Se alguém puder me ajudar aqui fico grato
Assunto:
função demanda
Autor:
ssousa3 - Seg Abr 04, 2011 14:30
Gente alguém por favor me ensine a calcular a fórmula da função demanda

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



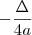 . Esse valor ficará em função do coeficiente c.
. Esse valor ficará em função do coeficiente c.
![f(x+1)-f(x)=6x-2
[tex]
a{(x+1)}^{2}+b(x+1)+c-a{x}^{2}-bx-c=6x-2 f(x+1)-f(x)=6x-2
[tex]
a{(x+1)}^{2}+b(x+1)+c-a{x}^{2}-bx-c=6x-2](/latexrender/pictures/abb3718cb039122094dcb3d793ac73ae.png)