Nessas questões, ele já nos dá f'(x).

Encontrei:
- pontos críticos: x=1
- Intervalo onde é crescente ou decrescente: crescente para x>1 e decrescente para x <1 (correto?)
- Mínimo e máximo local:
Como encontrar?




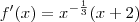



Fabio Cabral escreveu:Ele quer o ponto crítico da função f(x).
Mas ao invés de dar f(x) para encontrarmos f'(x), já deu f'(x) direto. Entende?
 ?".
?".Fabio Cabral escreveu:Não consigo 'simplificar' essa expressão (digamos assim).
Já tentei passar pra raíz, fazer distributiva.. enfim, várias coisas.
 . Mas, essa equação é a mesma que
. Mas, essa equação é a mesma que ![\frac{x+2}{\sqrt[3]{x}} = 0 \frac{x+2}{\sqrt[3]{x}} = 0](/latexrender/pictures/d40b1fe46fcd11c811d507e360ddc869.png) .
.
Voltar para Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 4 visitantes


 , avisa que eu resolvo.
, avisa que eu resolvo.

