 por Fabio Cabral » Sex Jun 17, 2011 12:23
por Fabio Cabral » Sex Jun 17, 2011 12:23
Até agora, eu tinha apenas pegado questões simples. Porém agora complicou. São 3 questões.
Nessas questões, ele já nos dá f'(x).

Encontrei:
- pontos críticos: x=1
- Intervalo onde é crescente ou decrescente: crescente para x>1 e decrescente para x <1
(correto?)- Mínimo e máximo local:
Como encontrar?
" A Matemática não mente. Mente quem faz mau uso dela. " - Albert Einstein
-
Fabio Cabral
- Colaborador Voluntário

-
- Mensagens: 122
- Registrado em: Qua Out 06, 2010 11:33
- Localização: Brasília-DF
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Ciência da computação
- Andamento: cursando
 por LuizAquino » Sex Jun 17, 2011 12:56
por LuizAquino » Sex Jun 17, 2011 12:56
Eu recomendo que assista as
vídeo-aulas:
- 19. Cálculo I - Máximo e Mínimo de Funções.
- 20. Cálculo I - Crescimento, Decrescimento e Concavidade do Gráfico de Funções.
- 21. Cálculo I - Teste da Primeira e da Segunda Derivada.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por Fabio Cabral » Dom Jun 19, 2011 15:37
por Fabio Cabral » Dom Jun 19, 2011 15:37
Como encontro o ponto crítico de
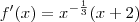
Não consigo simplificar essa expressão, de modo a conseguir encontrar o ponto crítico.
ps.: Essa ja é a derivada.
Grato.
" A Matemática não mente. Mente quem faz mau uso dela. " - Albert Einstein
-
Fabio Cabral
- Colaborador Voluntário

-
- Mensagens: 122
- Registrado em: Qua Out 06, 2010 11:33
- Localização: Brasília-DF
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Ciência da computação
- Andamento: cursando
 por LuizAquino » Dom Jun 19, 2011 16:12
por LuizAquino » Dom Jun 19, 2011 16:12
Qual é o texto original do exercício? É solicitado o ponto crítico da função f ou da função f'?
Se você deseja saber o ponto crítico de f, então você precisa resolver a equação f'(x) = 0.
Por outro lado, se você deseja saber o ponto crítico de f', então você precisa resolver a equação f''(x) = 0.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por Fabio Cabral » Dom Jun 19, 2011 16:17
por Fabio Cabral » Dom Jun 19, 2011 16:17
Veja, Luíz.
Ele quer o ponto crítico da função f(x).
Mas ao invés de dar f(x) para encontrarmos f'(x), já deu f'(x) direto. Entende?
Sim, eu sei que para achar tenho que fazer f'(x)=0. Não consigo 'simplificar' essa expressão (digamos assim).
Já tentei passar pra raíz, fazer distributiva.. enfim, várias coisas.
Att,
" A Matemática não mente. Mente quem faz mau uso dela. " - Albert Einstein
-
Fabio Cabral
- Colaborador Voluntário

-
- Mensagens: 122
- Registrado em: Qua Out 06, 2010 11:33
- Localização: Brasília-DF
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Ciência da computação
- Andamento: cursando
 por LuizAquino » Dom Jun 19, 2011 16:25
por LuizAquino » Dom Jun 19, 2011 16:25
Fabio Cabral escreveu:Ele quer o ponto crítico da função f(x).
Mas ao invés de dar f(x) para encontrarmos f'(x), já deu f'(x) direto. Entende?
Sendo assim, você deveria ter escrito algo como: "Como encontro o ponto crítico de f sabendo que

?".
Por favor, procure ser mais claro da próxima vez.
Fabio Cabral escreveu:Não consigo 'simplificar' essa expressão (digamos assim).
Já tentei passar pra raíz, fazer distributiva.. enfim, várias coisas.
Não há mistério algum. Você precisa resolver a equação

. Mas, essa equação é a mesma que
![\frac{x+2}{\sqrt[3]{x}} = 0 \frac{x+2}{\sqrt[3]{x}} = 0](/latexrender/pictures/d40b1fe46fcd11c811d507e360ddc869.png)
.
Agora, basta terminar o exercício.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Ponto Crítico e Ponto de Inflexão e intervalos] Dúvidas em
por Andre Lopes » Qua Set 26, 2012 00:37
- 2 Respostas
- 3378 Exibições
- Última mensagem por MarceloFantini

Qui Set 27, 2012 06:56
Cálculo: Limites, Derivadas e Integrais
-
- [ponto critico]duvida sobre achar o ponto critico
por nayra suelen » Dom Mai 27, 2012 19:38
- 2 Respostas
- 2437 Exibições
- Última mensagem por nayra suelen

Qua Mai 30, 2012 13:23
Cálculo: Limites, Derivadas e Integrais
-
- derivadas ponto critico
 por eulercx » Ter Jan 26, 2016 11:54
por eulercx » Ter Jan 26, 2016 11:54
- 2 Respostas
- 2296 Exibições
- Última mensagem por adauto martins

Qui Jan 28, 2016 10:09
Cálculo: Limites, Derivadas e Integrais
-
- [Ponto Crítico] Dificuldade com Função de 2 Variáveis
por Guilhermeds » Qua Mai 30, 2012 16:40
- 2 Respostas
- 3179 Exibições
- Última mensagem por Guilhermeds

Qua Mai 30, 2012 17:39
Cálculo: Limites, Derivadas e Integrais
-
- [Derivada] Derivadas parciais e ponto crítico
por Mell » Dom Jul 07, 2013 10:24
- 1 Respostas
- 1916 Exibições
- Última mensagem por hygorvv

Seg Jul 08, 2013 07:11
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 3 visitantes
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.





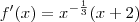



 ?".
?". . Mas, essa equação é a mesma que
. Mas, essa equação é a mesma que ![\frac{x+2}{\sqrt[3]{x}} = 0 \frac{x+2}{\sqrt[3]{x}} = 0](/latexrender/pictures/d40b1fe46fcd11c811d507e360ddc869.png) .
.