 por SheylaTamarossi » Dom Jun 12, 2011 11:19
por SheylaTamarossi » Dom Jun 12, 2011 11:19
Use a regra de L’Hopital para determinar o limite.

Resolvendo a questão, cheguei ao seguinte resultado:

Minha dúvida é: Será que isso está certo? Tenho certa dificuldade nos sinais...
Se estiver, já posso aplicar o limite ou continuo fatorando?
Obrigada!
-
SheylaTamarossi
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Dom Jun 12, 2011 10:50
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: 3° ano
- Andamento: cursando
 por LuizAquino » Dom Jun 12, 2011 12:12
por LuizAquino » Dom Jun 12, 2011 12:12
Reveja a sua resolução. Lembre-se que:
(i)
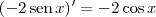
.
(ii)
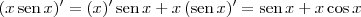
.
Além disso, vale destacar que você pode aplicar a Regra de L'Hôpital enquanto o limite tiver uma indeterminação 0/0 ou infinito/infinito.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por Fabio Cabral » Seg Jun 13, 2011 10:54
por Fabio Cabral » Seg Jun 13, 2011 10:54
Bom dia.
Para derivar essas duas funções acima, aplique a regra da cadeia.
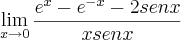

Note que você ainda terá uma indeterminação do tipo

.
Derive a função novamente:
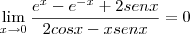
Editado pela última vez por
Fabio Cabral em Seg Jun 13, 2011 11:46, em um total de 1 vez.
" A Matemática não mente. Mente quem faz mau uso dela. " - Albert Einstein
-
Fabio Cabral
- Colaborador Voluntário

-
- Mensagens: 122
- Registrado em: Qua Out 06, 2010 11:33
- Localização: Brasília-DF
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Ciência da computação
- Andamento: cursando
 por LuizAquino » Seg Jun 13, 2011 11:26
por LuizAquino » Seg Jun 13, 2011 11:26
Fabio Cabral escreveu: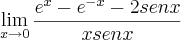

Cuidado com a escrita!
Note, por exemplo, que
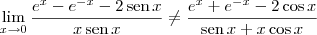
.
O correto é:
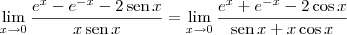
.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por Fabio Cabral » Seg Jun 13, 2011 11:45
por Fabio Cabral » Seg Jun 13, 2011 11:45
Certo, Luiz. Corrigi.
Sempre escrever o Limite.
Obrigado!

" A Matemática não mente. Mente quem faz mau uso dela. " - Albert Einstein
-
Fabio Cabral
- Colaborador Voluntário

-
- Mensagens: 122
- Registrado em: Qua Out 06, 2010 11:33
- Localização: Brasília-DF
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Ciência da computação
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Derivadas] Derivadas com definição de limites
 por concurseironf » Sex Set 05, 2014 18:11
por concurseironf » Sex Set 05, 2014 18:11
- 1 Respostas
- 1994 Exibições
- Última mensagem por DanielFerreira

Dom Set 07, 2014 22:18
Cálculo: Limites, Derivadas e Integrais
-
- Derivadas, Limites
por Grasi » Qui Jun 25, 2009 00:12
- 1 Respostas
- 3300 Exibições
- Última mensagem por Molina

Qui Jun 25, 2009 11:05
Cálculo: Limites, Derivadas e Integrais
-
- Derivadas, Limites
por Grasi » Qui Jun 25, 2009 00:15
- 1 Respostas
- 2550 Exibições
- Última mensagem por Molina

Qui Jun 25, 2009 11:30
Cálculo: Limites, Derivadas e Integrais
-
- Derivadas, Limites
por Grasi » Qui Jun 25, 2009 00:16
- 1 Respostas
- 2082 Exibições
- Última mensagem por Neperiano

Sáb Set 17, 2011 15:24
Cálculo: Limites, Derivadas e Integrais
-
- Derivadas, Limites
por Grasi » Qui Jun 25, 2009 00:18
- 0 Respostas
- 1439 Exibições
- Última mensagem por Grasi

Qui Jun 25, 2009 00:18
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 4 visitantes
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.






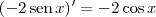 .
.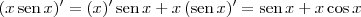 .
.
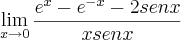

 .
.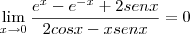

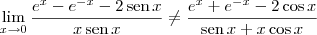 .
.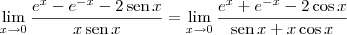 .
.
