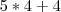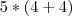por theSinister » Dom Jun 12, 2011 19:17
por theSinister » Dom Jun 12, 2011 19:17
Como simplificar a expressão :
E= (v28-v24)^4 . (v28+v24)^4 obs:. atribua "v" ao simbolo de raiz quadrada.
simplificando as raizes eu sei que vai fikar (2v7- 2v6)^4 . (2v7+2v6)^4, porem n consegui evoluir mais.
help-me
-
theSinister
- Usuário Dedicado

-
- Mensagens: 41
- Registrado em: Sáb Abr 23, 2011 18:36
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por Molina » Dom Jun 12, 2011 21:53
por Molina » Dom Jun 12, 2011 21:53
Boa noite.
Para as próximas edições, tente usar o
Editor de fórmulas. Qualquer dúvida quanto a seu uso pode ser tirada comigo ou
aqui.
Quanto a sua dúvida, vou mostrar um outro caminho:
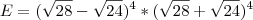 Pela propriedade de potência, temos que (a*b)^n = a^n * b^n:
Pela propriedade de potência, temos que (a*b)^n = a^n * b^n:![E= [(\sqrt{28}-\sqrt{24}) * (\sqrt{28}+\sqrt{24})]^4 E= [(\sqrt{28}-\sqrt{24}) * (\sqrt{28}+\sqrt{24})]^4](/latexrender/pictures/6a434e85e29b932b174a194dadcc5505.png) Fazendo a distributiva:
Fazendo a distributiva:![E= [28+\sqrt{28}\sqrt{24} - \sqrt{28}\sqrt{24} - 24]^4 E= [28+\sqrt{28}\sqrt{24} - \sqrt{28}\sqrt{24} - 24]^4](/latexrender/pictures/114e16d06aa7b129d966e3a1e58b6010.png)



Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por theSinister » Seg Jun 13, 2011 00:02
por theSinister » Seg Jun 13, 2011 00:02
VLW cara, bem mais facil assim hehehe. enquanto ao editor de formulas ,tentei colocar essa expressão nele mas não consegui, vou precisar de ajuda
flw!!
-
theSinister
- Usuário Dedicado

-
- Mensagens: 41
- Registrado em: Sáb Abr 23, 2011 18:36
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por Molina » Seg Jun 13, 2011 00:17
por Molina » Seg Jun 13, 2011 00:17
theSinister escreveu:VLW cara, bem mais facil assim hehehe. enquanto ao editor de formulas ,tentei colocar essa expressão nele mas não consegui, vou precisar de ajuda
flw!!
Para facilitar teu aprendizado, vou disponibilizar os códigos que usei neste meu último post:
- Código: Selecionar todos
[tex]E= (\sqrt{28}-\sqrt{24})^4 * (\sqrt{28}+\sqrt{24})^4[/tex]
[tex]E= [(\sqrt{28}-\sqrt{24}) * (\sqrt{28}+\sqrt{24})]^4[/tex]
[tex]E= [28+\sqrt{28}\sqrt{24} - \sqrt{28}\sqrt{24} - 24]^4[/tex]
[tex]E= 4^4[/tex]
[tex]E= 256[/tex]

Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por theSinister » Seg Jun 13, 2011 00:31
por theSinister » Seg Jun 13, 2011 00:31
ops agora que eu vi, aqui no gabarito a resposta está 64,e agora?
-
theSinister
- Usuário Dedicado

-
- Mensagens: 41
- Registrado em: Sáb Abr 23, 2011 18:36
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por Molina » Seg Jun 13, 2011 00:46
por Molina » Seg Jun 13, 2011 00:46
theSinister escreveu:ops agora que eu vi, aqui no gabarito a resposta está 64,e agora?
Estranho... Confira se não há nenhum erro de digitação quando você escreveu aqui.
Quanto a minha resposta, o
wolframalpha confirma isso!

Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por theSinister » Seg Jun 13, 2011 12:34
por theSinister » Seg Jun 13, 2011 12:34
BLZ cara , gostaria de aproveitar esse post para tirar outra duvida
Existe algum tipo de hierarquia para resolver as expressões ? ouvi dizer que primeiramenre resolve-se a exponenciação (se houver é claro) depois a radiciação, em seguida a divisão ,depois a multiplicação e por ultimo resolve-se as operações de subtração e adição.
-
theSinister
- Usuário Dedicado

-
- Mensagens: 41
- Registrado em: Sáb Abr 23, 2011 18:36
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por Molina » Seg Jun 13, 2011 12:42
por Molina » Seg Jun 13, 2011 12:42
Bom dia!
theSinister escreveu:BLZ cara , gostaria de aproveitar esse post para tirar outra duvida
Existe algum tipo de hierarquia para resolver as expressões ? ouvi dizer que primeiramenre resolve-se a exponenciação (se houver é claro) depois a radiciação, em seguida a divisão ,depois a multiplicação e por ultimo resolve-se as operações de subtração e adição.
É isso mesmo. Esta hierarquia precisa ser respeitada para que seja possível encontrar o valor correto. Uma "quebra" dessa regra já daria um valor diferente. Vou dar um exemplo:
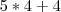
O resultado correto é 24, pois 5*4 = 20 + 4 = 24. Mas se eu não usar esta hierarquia e fizer primeiramente a soma e depois a multiplicação, o resultado dará 40, veja: 5*8 = 40.
Então tem que ser respeitado sim!
Você precisa também tomar cuidado com parênteses, colchetes e chaves, que passam na frente de toda essa hierarquia dita por você. Exemplo:
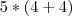
Agora eu faço primeiramente o que está dentro do parênteses e meu resultado é de fato 40.

Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por theSinister » Seg Jun 13, 2011 15:10
por theSinister » Seg Jun 13, 2011 15:10
Vlw , agora não vou mais me perder hehheh
-
theSinister
- Usuário Dedicado

-
- Mensagens: 41
- Registrado em: Sáb Abr 23, 2011 18:36
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- simplificar expressões com radicais II
por theSinister » Sex Jun 17, 2011 18:42
- 4 Respostas
- 3553 Exibições
- Última mensagem por theSinister

Sáb Jun 18, 2011 23:49
Álgebra Elementar
-
- LIMITE COM RADICAIS como fatorar ou simplificar
por pedroklein+1978 » Ter Abr 25, 2017 18:42
- 0 Respostas
- 2861 Exibições
- Última mensagem por pedroklein+1978

Ter Abr 25, 2017 18:42
Cálculo: Limites, Derivadas e Integrais
-
- Simplificar
por Sandy26 » Ter Abr 27, 2010 14:35
- 5 Respostas
- 3172 Exibições
- Última mensagem por MarceloFantini

Qui Abr 29, 2010 18:29
Cálculo: Limites, Derivadas e Integrais
-
- Radicais
por agfp5 » Sáb Out 30, 2010 08:50
- 2 Respostas
- 2333 Exibições
- Última mensagem por agfp5

Sáb Out 30, 2010 09:10
Geometria Plana
-
- Simplificar
por victorleme » Qua Mai 04, 2011 20:06
- 4 Respostas
- 2518 Exibições
- Última mensagem por victorleme

Qui Mai 05, 2011 18:56
Polinômios
Usuários navegando neste fórum: Nenhum usuário registrado e 3 visitantes
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



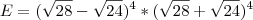
![E= [(\sqrt{28}-\sqrt{24}) * (\sqrt{28}+\sqrt{24})]^4 E= [(\sqrt{28}-\sqrt{24}) * (\sqrt{28}+\sqrt{24})]^4](/latexrender/pictures/6a434e85e29b932b174a194dadcc5505.png)
![E= [28+\sqrt{28}\sqrt{24} - \sqrt{28}\sqrt{24} - 24]^4 E= [28+\sqrt{28}\sqrt{24} - \sqrt{28}\sqrt{24} - 24]^4](/latexrender/pictures/114e16d06aa7b129d966e3a1e58b6010.png)