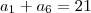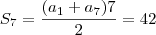por crfsatisfaction » Qui Jun 09, 2011 00:59
por crfsatisfaction » Qui Jun 09, 2011 00:59
E ai pessoal,tentei fazer uma questao de P.A e nao consegui terminar,cheguei em um sistema mas não sei se esta correto
A questa é a seguinte:
Se a soma dos 6 primeiros termos de uma P.A.é 21 e o sétimo termo é o triplo da soma do terceiro com o quarto termo,então o primeiro termo desta progressão é:
primerira informação:
a1+a2+a3+a4+a5+a6=21
a1+a1+r+a1+2r+a1+3r+a1+4r+a1+5r=21
6a1+15r=21
segunda informação:
a7=3(a3+a4)
a1+6r=3(a1+2r+a1+3r)
a1+6r=3(2a1+5r)
a1+6r=6a1+15r
a1+6r-6a1-15r=0
-5a1-9r
E apareceu este sistema:
6a1+15r
-5a1-9r
Apartir dai nao consegui resolver mas mesmo assim ta estranho,gostaria que alguem me ajudasse.
A resposta é -9
-
crfsatisfaction
- Novo Usuário

-
- Mensagens: 5
- Registrado em: Qui Jun 09, 2011 00:22
- Formação Escolar: GRADUAÇÃO
- Área/Curso: licenciatura em letras portugues/ingles
- Andamento: cursando
 por FilipeCaceres » Qui Jun 09, 2011 10:44
por FilipeCaceres » Qui Jun 09, 2011 10:44
-
FilipeCaceres
- Colaborador Voluntário

-
- Mensagens: 351
- Registrado em: Dom Out 31, 2010 21:43
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Tec. Mecatrônica
- Andamento: formado
 por crfsatisfaction » Sex Jun 10, 2011 00:59
por crfsatisfaction » Sex Jun 10, 2011 00:59
muito obrigado, me ajudou bastante,nao sabia da propriedade dos termos equidistantes,sua colaboração foi significativa
abraço
-
crfsatisfaction
- Novo Usuário

-
- Mensagens: 5
- Registrado em: Qui Jun 09, 2011 00:22
- Formação Escolar: GRADUAÇÃO
- Área/Curso: licenciatura em letras portugues/ingles
- Andamento: cursando
Voltar para Sequências
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Primeiro Termo da P.G.
por Cleyson007 » Seg Out 12, 2009 17:14
- 1 Respostas
- 2074 Exibições
- Última mensagem por Molina

Seg Out 12, 2009 23:30
Progressões
-
- Primeiro problema
por gabimucedola » Qui Mar 25, 2010 21:44
- 3 Respostas
- 1645 Exibições
- Última mensagem por gabimucedola

Seg Mar 29, 2010 14:21
Álgebra Elementar
-
- Redyção ao primeiro quadrante.
por rodsales » Seg Out 12, 2009 09:24
- 1 Respostas
- 1185 Exibições
- Última mensagem por Marcampucio

Seg Out 12, 2009 11:49
Trigonometria
-
- Função de Primeiro Grau
por Najyh » Seg Mai 03, 2010 23:22
- 3 Respostas
- 5039 Exibições
- Última mensagem por MarceloFantini

Ter Mai 04, 2010 22:41
Funções
-
- Equação do primeiro grau
por isaiaspereira » Qui Jan 27, 2011 00:53
- 3 Respostas
- 2894 Exibições
- Última mensagem por Elcioschin

Qui Jan 27, 2011 14:02
Álgebra Elementar
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.