Oi pessoal, como vão.
To estudando Geometria Analítica na facul e to com dificuldade de descobrir um vetor normal a um plano dado. Como fazer isso se eu tiver a equação vetorial de um plano? Eu li alguma coisa sobre colocar a equação na forma geral e assim pegar os coeficientes dela.
Ex: 2x+5y+z+2=0
aí o vetor seria:
(2,5,1)
É isso mesmo ou tem outro modo?
Até mais e obrigado desde ja


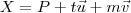 , sendo
, sendo  e
e  são chamados de
são chamados de  é um vetor normal ao plano dado pela equação anterior, então
é um vetor normal ao plano dado pela equação anterior, então  e
e  .
.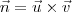 .
.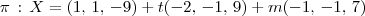 .
.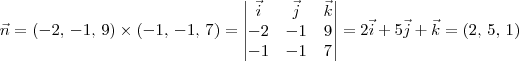 .
.
 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.