 por suziquim » Qua Jun 08, 2011 13:18
por suziquim » Qua Jun 08, 2011 13:18
Tem um exercício resolvido no livro, mas não entendi a resolução da integral, gostaria que alguém me ajudasse a entender:

=
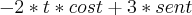
-
suziquim
- Usuário Ativo

-
- Mensagens: 10
- Registrado em: Qui Mai 05, 2011 11:53
- Formação Escolar: GRADUAÇÃO
- Área/Curso: engenharia
- Andamento: cursando
 por LuizAquino » Qua Jun 08, 2011 15:59
por LuizAquino » Qua Jun 08, 2011 15:59
Descreva a parte da resolução que você não entendeu.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por suziquim » Qua Jun 08, 2011 16:17
por suziquim » Qua Jun 08, 2011 16:17
Fazendo

=
![[sen t]+ \int_{-1}^{2}2t*sen t dt [sen t]+ \int_{-1}^{2}2t*sen t dt](/latexrender/pictures/0acc53e850a44410768c96dfbba16c07.png)
ess segunda integral eu não sei resolver
-
suziquim
- Usuário Ativo

-
- Mensagens: 10
- Registrado em: Qui Mai 05, 2011 11:53
- Formação Escolar: GRADUAÇÃO
- Área/Curso: engenharia
- Andamento: cursando
 por MarceloFantini » Qua Jun 08, 2011 17:59
por MarceloFantini » Qua Jun 08, 2011 17:59
Resolva como integração por partes: chame

e

.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por suziquim » Qui Jun 09, 2011 12:04
por suziquim » Qui Jun 09, 2011 12:04
Obrigada
-
suziquim
- Usuário Ativo

-
- Mensagens: 10
- Registrado em: Qui Mai 05, 2011 11:53
- Formação Escolar: GRADUAÇÃO
- Área/Curso: engenharia
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Integral - Resolução de integral indefinida.
por brunoisoppo » Qui Mar 03, 2016 15:26
- 0 Respostas
- 3445 Exibições
- Última mensagem por brunoisoppo

Qui Mar 03, 2016 15:26
Cálculo: Limites, Derivadas e Integrais
-
- Resolução de Integral -
por vmouc » Dom Ago 21, 2011 15:01
- 2 Respostas
- 1814 Exibições
- Última mensagem por Neperiano

Dom Ago 21, 2011 15:25
Cálculo: Limites, Derivadas e Integrais
-
- [Resolução de integral]
por adomingues » Sex Jan 20, 2012 16:45
- 2 Respostas
- 1810 Exibições
- Última mensagem por ant_dii

Sáb Jan 21, 2012 02:39
Cálculo: Limites, Derivadas e Integrais
-
- RESOLUÇÃO DE INTEGRAL
por anselmojr97 » Ter Set 22, 2015 11:06
- 2 Respostas
- 2257 Exibições
- Última mensagem por anselmojr97

Ter Set 22, 2015 11:45
Cálculo: Limites, Derivadas e Integrais
-
- resolução derivada integral
por MARCIOESTUDIOSO » Seg Fev 14, 2011 10:33
- 4 Respostas
- 4081 Exibições
- Última mensagem por LuizAquino

Ter Fev 15, 2011 14:37
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 4 visitantes
Assunto:
Exercicios de polinomios
Autor:
shaft - Qua Jun 30, 2010 17:30

Então, o exercicio pede para encontrar

.
Bom, tentei resolver a questão acima desenvolvendo as duas partes em ( )...Logo dps cheguei em um resultado q nao soube o q fazer mais.
Se vcs puderem ajudar !
Assunto:
Exercicios de polinomios
Autor:
Douglasm - Qua Jun 30, 2010 17:53
Bom, se desenvolvermos isso, encontramos:

Para que os polinômios sejam iguais, seus respectivos coeficientes devem ser iguais (ax = bx ; ax² = bx², etc.):


Somando a primeira e a segunda equação:

Finalmente:

Até a próxima.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 =
=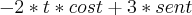

 =
=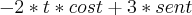



![[sen t]+ \int_{-1}^{2}2t*sen t dt [sen t]+ \int_{-1}^{2}2t*sen t dt](/latexrender/pictures/0acc53e850a44410768c96dfbba16c07.png)




 .
.



