Meu professor fez essa derivada no quadro mas nao intendi nada... alguem pode me explicar?!

Tipo ele fez por regra da cadeia mas primeiro ele pôs a funçao com exponencial assim:
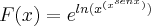
eu sei que essa funçao e^ln ... é a mesma coisa que a funçao la em cima, no entanto nao intendo no que isso ajuda pra fazer a questao e consequentemente isso confundiu todo resto da questao. Tentei fazer normal por regra da cadeia mas o resultado fico algo estranho e longe da resposta que ele (professor) chegou. Desculpe os varios erros de gramatica... tava com pressa xD.
 pra quem leu !! e
pra quem leu !! e 
 pra quem leu e respondeu
pra quem leu e respondeu 


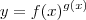 , com
, com 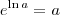 e que
e que  .
.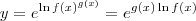 .
.![y^\prime = \left[e^{g(x)\ln f(x)}\right]^\prime = \left[g(x)\ln f(x)\right]^\prime e^{g(x)\ln f(x)} = \left[g(x)\ln f(x)\right]^\prime f(x)^{g(x)}} y^\prime = \left[e^{g(x)\ln f(x)}\right]^\prime = \left[g(x)\ln f(x)\right]^\prime e^{g(x)\ln f(x)} = \left[g(x)\ln f(x)\right]^\prime f(x)^{g(x)}}](/latexrender/pictures/98377d88eb36f89e1241ecf0f67bfc7f.png) . (Lembrete: pela Regra da Cadeia, temos que
. (Lembrete: pela Regra da Cadeia, temos que ![[e^u]^\prime = u^\prime e^u [e^u]^\prime = u^\prime e^u](/latexrender/pictures/df80f23670eae9f57797b16b8f0a96ec.png) .)
.)![\left[f(x)^{g(x)}\right]^\prime = \left[g(x)\ln f(x)\right]^\prime f(x)^{g(x)} \left[f(x)^{g(x)}\right]^\prime = \left[g(x)\ln f(x)\right]^\prime f(x)^{g(x)}](/latexrender/pictures/ce83c48ba6bea3871cc8d7c3ee01c8f0.png) .
. . Fazendo
. Fazendo  e
e  temos que
temos que 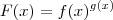 . Agora basta aplicar a regra acima.
. Agora basta aplicar a regra acima.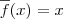 e
e 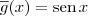 temos que
temos que 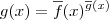 . Daí basta aplicar a regra novamente para essa função.
. Daí basta aplicar a regra novamente para essa função.

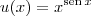 é verdadeiro que
é verdadeiro que 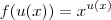 ?
?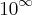 , vlw pela ajuda msm.
, vlw pela ajuda msm.
 .
.
 :
: