Estou com dúvida em duas questões:
1. O seno dos ângulos iguais de um triângulo isósceles vale 3/5, e o perímetro, 9 m. Calcule o valor de sua área.
Fiz a figura e sei que senB = SenC = 3/5 e que a + b + c = 9 ou a + 2b = 9. já tentei colocar a altura e calcular através do sen = cateto oposto sobre a hipotenusa, mas não estou conseguindo.Também tentei pela fórmula da área:
 . Tem uma dica?
. Tem uma dica?2. Num triângulo qualquer, A vale 60 graus e é o ângulo formado pelos lados b = (
![\sqrt[]{3}-1 \sqrt[]{3}-1](/latexrender/pictures/4b515e5abee7652a0ffbdc40bc203154.png) )m e c = 1 m. Calcule o valor do ângulo B, oposto ao lado b.
)m e c = 1 m. Calcule o valor do ângulo B, oposto ao lado b.Fiz a figura de tentei encontrar através da lei do cosseno:
 e encontrei
e encontrei ![{a}^{2}= 6-3\sqrt[]{3} {a}^{2}= 6-3\sqrt[]{3}](/latexrender/pictures/5ae48828fecf21a20e49d990dc4cd806.png) . Aí tentei substituir no
. Aí tentei substituir no  , mas não encontrei. Este é o caminho?
, mas não encontrei. Este é o caminho?Obrigada!


 e
e  dos lados.
dos lados. , respectivamente, anote as medidas dos lados dos triângulos retângulos formados (há um par). Atenção pois um dos catetos é
, respectivamente, anote as medidas dos lados dos triângulos retângulos formados (há um par). Atenção pois um dos catetos é 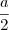 ;
; os ângulos de mesma medida, a partir do triângulo retângulo, note que:
os ângulos de mesma medida, a partir do triângulo retângulo, note que:  . Utilize aqui o dado do enunciado para escrever
. Utilize aqui o dado do enunciado para escrever 

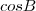 .
.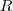 da circunferência circunscrita ao triângulo.
da circunferência circunscrita ao triângulo.
 , substituindo
, substituindo 
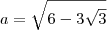 .
.![{a}^{2}= {b}^{2}+{c}^{2}- 2bccosA
{a}^{2}= (\sqrt[]{3}-1){}^{2}+1-2(\sqrt[]{3}-1).1.cos60
{a}^{2}= 6 - 3\sqrt[]{3}
a = \sqrt[]{6 - 3\sqrt[]{3}}
\frac{a}{senA}= 2R
\sqrt[]{6-3\sqrt[]{3}}= 2R. \frac{2}{\sqrt[]{3}}
elevando os dois ao quadrado:
6 - 3\sqrt[]{3}= \frac{16}{3}.R
R= \frac{18 - 9\sqrt[]{3}}{16}
\frac{b}{senB}= 2R
\frac{\sqrt[]{3}-1}{senB}= \frac{18-9\sqrt[]{3}}{16}
senB = \frac{8(\sqrt[]{3}-1}{9} {a}^{2}= {b}^{2}+{c}^{2}- 2bccosA
{a}^{2}= (\sqrt[]{3}-1){}^{2}+1-2(\sqrt[]{3}-1).1.cos60
{a}^{2}= 6 - 3\sqrt[]{3}
a = \sqrt[]{6 - 3\sqrt[]{3}}
\frac{a}{senA}= 2R
\sqrt[]{6-3\sqrt[]{3}}= 2R. \frac{2}{\sqrt[]{3}}
elevando os dois ao quadrado:
6 - 3\sqrt[]{3}= \frac{16}{3}.R
R= \frac{18 - 9\sqrt[]{3}}{16}
\frac{b}{senB}= 2R
\frac{\sqrt[]{3}-1}{senB}= \frac{18-9\sqrt[]{3}}{16}
senB = \frac{8(\sqrt[]{3}-1}{9}](/latexrender/pictures/5f011214d8d9edb95ed64f6f27aeb577.png)
 encontrei senB =
encontrei senB = ![\frac{\sqrt[]{3}-1}{2} \frac{\sqrt[]{3}-1}{2}](/latexrender/pictures/18d234b12d7859439e5e9edee82185d7.png) ; deu isso? E agora?
; deu isso? E agora?

![2R . \frac{\sqrt[]{3}}{2}= \sqrt[]{6-3\sqrt[]{3}}
R = \frac{\sqrt[]{6-3\sqrt[]{3}}}{\sqrt[]{3}}
racionalizando
R = \frac{\sqrt[]{18-9}}{3}
R = 1 2R . \frac{\sqrt[]{3}}{2}= \sqrt[]{6-3\sqrt[]{3}}
R = \frac{\sqrt[]{6-3\sqrt[]{3}}}{\sqrt[]{3}}
racionalizando
R = \frac{\sqrt[]{18-9}}{3}
R = 1](/latexrender/pictures/3d155df6965029b87d39a6d9927217a7.png)
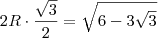

 de dentro da raiz quadrada "sumiu".
de dentro da raiz quadrada "sumiu".
![R= \sqrt[]{2-\sqrt[]{3}} R= \sqrt[]{2-\sqrt[]{3}}](/latexrender/pictures/a88ca2aa62079503bf861960a8f19841.png) aí, ficarei com:
aí, ficarei com:![\left(\frac{\sqrt[]{3}-1}{senB} \right) = 2. \sqrt[]{2-\sqrt[]{3}}
aí ficaria com senB = \left(\frac{\sqrt[]{3}-1}{2\sqrt[]{2-\sqrt[]{3}}} \right) \left(\frac{\sqrt[]{3}-1}{senB} \right) = 2. \sqrt[]{2-\sqrt[]{3}}
aí ficaria com senB = \left(\frac{\sqrt[]{3}-1}{2\sqrt[]{2-\sqrt[]{3}}} \right)](/latexrender/pictures/bff5f409a4c0384150c5854374799f62.png)

 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.