 por Rose » Ter Jun 07, 2011 00:25
por Rose » Ter Jun 07, 2011 00:25
Olá,
Estou tentando calcular este probelma, mas esta dificil!! Por exemplo, como vou fazer para achar o volume de água que deve ser passado do
vaso de menor raio para o outro a fim de que surja uma diferença de 26 cm entre os níveis
da água num e noutro vaso?
Não sei fazer! Me ajudem! O problema segue abaixo:
!) Em dois vasos cilíndricos, de eixo vertical, há água até a mesma altura; um dos
vasos tem raio 30 cm e o outro 45 cm. Qual é o volume de água que deve ser passado do
vaso de menor raio para o outro a fim de que surja uma diferença de 26 cm entre os níveis
da água num e noutro vaso?
-
Rose
- Usuário Ativo

-
- Mensagens: 22
- Registrado em: Qui Mai 15, 2008 14:13
- Área/Curso: Estudante
- Andamento: cursando
 por carlosalesouza » Ter Jun 07, 2011 01:44
por carlosalesouza » Ter Jun 07, 2011 01:44
Antes de começar... esse problema não exige logaritmo...
observemos o seguinte:
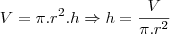
A altura inicial de ambos e a mesma...
Note que estamos procurando um volume x que, acrescido ao volume do cilindro mais largo e retirado do volume do cilindro mais estreito implique em variações das alturas que, somadas, representarão 26cm... ok?
Vemos, pela fórmula acima, que
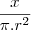
corresponderá ao impacto que um volume x terá no nível da água, correto?
Assim:

Ou seja, serão necessários
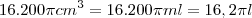
Esta é a quantidade de água que precisa ser transferida para ocasionar a diferença de altura desejada...
ok?
Um grande abraço
Carlos Alexandre
Ciências Contábeis - FECEA/PR
Matemática - UEPG/PR
-
carlosalesouza
- Colaborador Voluntário

-
- Mensagens: 103
- Registrado em: Sex Abr 29, 2011 17:28
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática -LIC
- Andamento: cursando
 por Rose » Ter Jun 07, 2011 14:04
por Rose » Ter Jun 07, 2011 14:04
Olá, Carlos!!
Muitíssimo obrigada!! Valeu mesmo!!Não tinha nenhuma idéia por onde começar a resolver este problema.
Abraços
-
Rose
- Usuário Ativo

-
- Mensagens: 22
- Registrado em: Qui Mai 15, 2008 14:13
- Área/Curso: Estudante
- Andamento: cursando
 por Angelica Abdalla » Ter Jul 12, 2011 21:33
por Angelica Abdalla » Ter Jul 12, 2011 21:33
Boa noite a todos,
Vou colocar o problema e a resoluçaõ que fiz. Vcs podem ver se aonde errei?
PROBLEMA:
Em dois vasos cilíndricos, de eixo vertical, há água até a mesma altura; um dos vasos tem raio 30 cm e o outro 45 cm. Qual é o volume de água que deve ser passado do vaso de menor raio para o outro a fim de que surja uma diferença de 26 cm entre os níveis da água num e noutro vaso?
1) Escreva as equações que correspondem à situação exposta no problema (e que, portanto, permita resolvê-lo), explicando claramente quais são os elementos envolvidos e qual o raciocínio usado para estabelecer tal equação.
2) Resolva as equações para obter a resposta à pergunta posta no problema.
Resolução:
Para resolvermos esse problema, vamos utilizar os conhecimentos de Geometria Espacial, sobre cilindros, no qual aplica-se no 2? ano do Ensino Médio.
Sejam R um círculo contido num plano ? e (XY) ? um segmento de uma reta s concorrente com ?. Denominamos Cilindro o conjunto dos pontos dos segmentos paralelos e congruentes a (XY) ? que têm uma extremidade em R e que estão num mesmo semi-espaço determinado por ?.
Para encontrarmos o volume do cilindro, precisamos conhecer o raio r de sua base, em vez que o volume é dado por:
V_cilindro=( área da base)×(altura)
Sabendo-se que a área da base de um cilindro é A_base=?r^2, logo, temos que o raio do cilindro é 30 cm.
Calculando a Área da base do primeiro cilindro:
A_base=??30?^2
A_base=900? cm²
Calculando o Volume:
Sabendo-se que para calcular o volume, utilizamos a seguinte fórmula:
V_cilindro=( área da base)×(altura)
Logo:
V_cilindro=900?.h cm³
Sabendo-se que a área da base de um cilindro é A_base=?r^2, logo, temos que o raio do segundo cilindro é 45 cm.
Calculando a Área da base do segundo cilindro:
A_base=??45?^2
A_base=2025? cm²
Calculando o Volume do segundo cilindro:
V_cilindro=( área da base)×(altura)
Logo:
V_cilindro=2025?.h cm³
Sabemos que h é a altura inicial dos dois cilindros
V_1, significa o volume inicial do primeiro cilindro: 900?h cm³
V_2, significa o volume inicial do segundo cilindro: 2025?h cm³
Chamaremos x o decréscimo do nível no primeiro vaso
e y acréscimo do nível no segundo vaso.
? V?_1', significa o volume do primeiro cilindro após a passagem do líquido: 900?(h-x)cm³
V_2', significa o volume do segundo cilindro após a passagem do líquido: 2025?(h+y) cm³
Logo:
V_1+V_2=V_1'+V_2'
Sendo que V_1=900? e V_1=900(h-x)volume após a passagem do líquido;
900?h+2025?h=900?(h-x)+2025?(h+y)
900?h+2025?h=900?h-900?x+2025?h+2025?y
900?h+2025?h-900?h-2025?h=-900?x+2025?y
900?x=2025?y
Sabendo-se que x+y=26, e substituindo o x teremos
x+y=26 ? x=26-y
900?x=2025?y ,simplificando ambos por 225 obteremos
4x=9y ? 4x/9=y
Resolvendo este sistema:
x=26-4x/9?9x/9=234/9-4x/9
9x+4x=234
13x=234
x=234/13
x=18 cm
Agora sabemos quanto vale o x, Substituindo na equação acima:
x=26-y
18=26-y
18-26=-y
-8=-y (×-1)
y=8 cm
Encontramos o valor de x e y e substituindo-os obteremos o valor do volume da água que sairá do recipiente de menor raio para o outro;
900?x cm³=2025?ycm³
900?×18=2025?×8
16.200? cm³=16200? cm³
Resposta: Podemos concluir que o volume de água que deve ser passado do cilindro de menor raio para o outro a fim de que surja uma diferença de 26 cm corresponde a 16200? cm³
-
Angelica Abdalla
- Novo Usuário

-
- Mensagens: 4
- Registrado em: Qua Jun 29, 2011 22:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: licenciatura em matemática
- Andamento: cursando
 por Angelica Abdalla » Ter Jul 12, 2011 21:34
por Angelica Abdalla » Ter Jul 12, 2011 21:34
Aguardo a resposta
-
Angelica Abdalla
- Novo Usuário

-
- Mensagens: 4
- Registrado em: Qua Jun 29, 2011 22:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: licenciatura em matemática
- Andamento: cursando
Voltar para Logaritmos
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Vasos Comunicantes] Física
por gustavoluiss » Qui Nov 24, 2011 10:25
- 0 Respostas
- 1783 Exibições
- Última mensagem por gustavoluiss

Qui Nov 24, 2011 10:25
Álgebra Elementar
-
- Escoamento de água
por Cleyson007 » Dom Jan 12, 2014 17:11
- 3 Respostas
- 6956 Exibições
- Última mensagem por Guilherme Pimentel

Qua Jan 15, 2014 04:55
Cálculo: Limites, Derivadas e Integrais
-
- Uma Torneira Lança água em um tanque
por Chicharito » Sáb Dez 08, 2012 15:26
- 1 Respostas
- 2522 Exibições
- Última mensagem por Russman

Sáb Dez 08, 2012 15:36
Cálculo: Limites, Derivadas e Integrais
-
- Ajuda Urgente
por Mimizinha » Qua Mar 19, 2008 16:45
- 2 Respostas
- 6236 Exibições
- Última mensagem por XILVANA

Qui Abr 11, 2013 13:58
Álgebra Elementar
-
- ajuda urgente
por pedro ferreira » Seg Ago 24, 2009 22:53
- 2 Respostas
- 6054 Exibições
- Última mensagem por pedro ferreira

Seg Ago 24, 2009 23:08
Funções
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
método de contagem
Autor:
sinuca147 - Seg Mai 25, 2009 09:10
Veja este exercício:
Se A = {

} e B = {

}, então o número de elementos A

B é:
Eu tentei resolver este exercício e achei a resposta "três", mas surgiram muitas dúvidas aqui durante a resolução.
Para determinar os elementos do conjunto A, eu tive de basicamente fazer um lista de vinte dividido por todos os números naturais maiores que zero e menores que vinte e um, finalmente identificando como elementos do conjunto A os números 1, 2, 4, 5, 10 e 20. Acho que procedi de maneira correta, mas fiquei pensando aqui se não existiria um método mais "sofisticado" e prático para que eu pudesse identificar ou ao menos contar o número de elementos do conjunto A, existe?
No processo de determinação dos elementos do conjunto B o que achei foi basicamente os múltiplos de cinco e seus opostos, daí me surgiram estas dúvidas:
existe oposto de zero?
existe inverso de zero?
zero é par, certo?
sendo x um número natural, -x é múltiplo de x?
sendo z um número inteiro negativo, z é múltiplo de z?
sendo z um número inteiro negativo, -z é múltiplo de z?
A resposta é 3?
Obrigado.
Assunto:
método de contagem
Autor:
Molina - Seg Mai 25, 2009 20:42
Boa noite, sinuca.
Se A = {

} você concorda que n só pode ser de 1 a 20? Já que pertence aos naturais?
Ou seja, quais são os divisores de 20? Eles são seis: 1, 2, 4, 5, 10 e 20.
Logo, o conjunto A é
A = {1, 2, 4, 5, 10, 20}
Se B = {

} você concorda que x será os múltiplos de 5 (positivos e negativos)? Já que m pertence ao conjunto Z?
Logo, o conjunto B é
B = {... , -25, -20, -15, -10, -5, 0, 5, 10, 15, 20, 25, ...
Feito isso precisamos ver os números que está em ambos os conjuntos, que são:
5, 10 e 20 (3 valores, como você achou).
Vou responder rapidamente suas dúvidas porque meu tempo está estourando. Qualquer dúvida, coloque aqui, ok?
sinuca147 escreveu:No processo de determinação dos elementos do conjunto B o que achei foi basicamente os múltiplos de cinco e seus opostos, daí me surgiram estas dúvidas:
existe oposto de zero? sim, é o próprio zero
existe inverso de zero? não, pois não há nenhum número que multiplicado por zero resulte em 1
zero é par, certo? sim, pois pode ser escrito da forma de 2n, onde n pertence aos inteiros
sendo x um número natural, -x é múltiplo de x? Sim, pois basta pegar x e multiplicar por -1 que encontramos -x
sendo z um número inteiro negativo, z é múltiplo de z? Sim, tais perguntando se todo número é multiplo de si mesmo
sendo z um número inteiro negativo, -z é múltiplo de z? Sim, pois basta pegar -z e multiplicar por -1 que encontramos x
A resposta é 3? Sim, pelo menos foi o que vimos a cima
Bom estudo,

Assunto:
método de contagem
Autor:
sinuca147 - Seg Mai 25, 2009 23:35
Obrigado, mas olha só este link
http://www.colegioweb.com.br/matematica ... ro-natural
neste link encontra-se a a frase:
Múltiplo de um número natural é qualquer número que possa ser obtido multiplicando o número natural por 0, 1, 2, 3, 4, 5, etc.
Para determinarmos os múltiplos de 15, por exemplo, devemos multiplicá-lo pela sucessão dos números naturais:
Ou seja, de acordo com este link -5 não poderia ser múltiplo de 5, assim como 5 não poderia ser múltiplo de -5, eu sempre achei que não interessava o sinal na questão dos múltiplos, assim como você me confirmou, mas e essa informação contrária deste site, tem alguma credibilidade?
Há e claro, a coisa mais bacana você esqueceu, quero saber se existe algum método de contagem diferente do manual neste caso:
Para determinar os elementos do conjunto A, eu tive de basicamente fazer um lista de vinte dividido por todos os números naturais maiores que zero e menores que vinte e um, finalmente identificando como elementos do conjunto A os números 1, 2, 4, 5, 10 e 20. Acho que procedi de maneira correta, mas fiquei pensando aqui se não existiria um método mais "sofisticado" e prático para que eu pudesse identificar ou ao menos contar o número de elementos do conjunto A, existe?
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


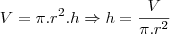
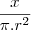 corresponderá ao impacto que um volume x terá no nível da água, correto?
corresponderá ao impacto que um volume x terá no nível da água, correto?
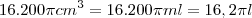


 } e B = {
} e B = { }, então o número de elementos A
}, então o número de elementos A  B é:
B é: