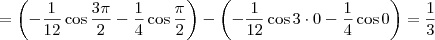por liviabgomes » Qua Jun 01, 2011 15:14
por liviabgomes » Qua Jun 01, 2011 15:14
Calcular a integral definida:

sen(x) cos²(x) dx=
a minha dúvida é: integral definida pode ser resolvida pelo método da substituição? Ou tenho que tentar resolver simplificando as fórmulas de seno e cosseno? Pelas transformações das fórmulas trigonométricas eu não consigo resolver. Podem me ajudar???
-
liviabgomes
- Usuário Ativo

-
- Mensagens: 15
- Registrado em: Seg Mai 30, 2011 16:04
- Formação Escolar: GRADUAÇÃO
- Área/Curso: matemática licenciatura
- Andamento: cursando
 por carlosalesouza » Qua Jun 01, 2011 16:30
por carlosalesouza » Qua Jun 01, 2011 16:30
vamos lá...

O que precisamos é integrar

vamos manipular seguindo as identidades trigonométricas...
Por favor, o Felipe que me corrija, pq trigonometria é a praia dele... hehhehehehe
![\\
sen(x).cos^2(x)\\
\left [sen(x).cos(x)\right ].cos(x)\\
\left [ \frac{1}{2}sen(2x)\right].cos(x)\\
\frac{1}{2}[sen(2x).cos(x)]\\
\frac{1}{2}\left[\frac{1}{2}(sen(x+2x)-sen(x-2x))\right ]\\
\frac{1}{4}[sen(3x)-sen(-x)]\\
\frac{1}{4}[sen(3x)+sen(x)] \\
sen(x).cos^2(x)\\
\left [sen(x).cos(x)\right ].cos(x)\\
\left [ \frac{1}{2}sen(2x)\right].cos(x)\\
\frac{1}{2}[sen(2x).cos(x)]\\
\frac{1}{2}\left[\frac{1}{2}(sen(x+2x)-sen(x-2x))\right ]\\
\frac{1}{4}[sen(3x)-sen(-x)]\\
\frac{1}{4}[sen(3x)+sen(x)]](/latexrender/pictures/a3553111601b4164756c1f342ca143a5.png)
Agora, integrando:
![\\
\displaystyle \int_0^\frac{\pi}{2}[sen(3x)+sen(x)]dx \\
\displaystyle \int_0^\frac{\pi}{2}[sen(3x)+sen(x)]dx](/latexrender/pictures/552ebeee3f2d9e58580e76e20ea4868f.png)
Como a integral de sen(x) é -cos(x), então:
![\\
\left [-cos(3x)-cos(x)\right ]_0^\frac{\pi}{2}\\
\left [-cos\left(3.\frac{\pi}{2}\right )-cos\left(\frac{\pi}{2}\right)\right ]-[-cos(3.0)-cos(0)]\\ \\
\left [-cos(3x)-cos(x)\right ]_0^\frac{\pi}{2}\\
\left [-cos\left(3.\frac{\pi}{2}\right )-cos\left(\frac{\pi}{2}\right)\right ]-[-cos(3.0)-cos(0)]\\](/latexrender/pictures/88d788c966f6b5ee276e788add593252.png)
bem...

Assim:
![\\
\left [-(0)-(0)\right ]-\left [-(1)-(1)\right ]\\
0-(-2) = 2 \\
\left [-(0)-(0)\right ]-\left [-(1)-(1)\right ]\\
0-(-2) = 2](/latexrender/pictures/9ff3f3fe5b993d4ab4f3b3d746b34351.png)
Como disse, espero o amparo dos caros colegas mais familiarizados com a trigonometria pra ver se não cometi algum deslize... mas, me parece certo...
Um grande abraço
Carlos Alexandre
Ciências Contábeis - FECEA/PR
Matemática - UEPG/PR
-
carlosalesouza
- Colaborador Voluntário

-
- Mensagens: 103
- Registrado em: Sex Abr 29, 2011 17:28
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática -LIC
- Andamento: cursando
 por LuizAquino » Qua Jun 01, 2011 16:36
por LuizAquino » Qua Jun 01, 2011 16:36
Nesse exercício em específico, a solução é mais simples.
Tomando-se u = cos x, temos que du = - sen x dx.
Desse modo, temos que:
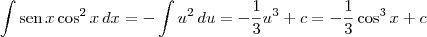
.
Observaçãocarlosalesouza,
Lembre-se que

, com
a real não nulo.
Além disso, você esqueceu da constante 1/4 no cálculo da integral.
Editado pela última vez por
LuizAquino em Qua Jun 01, 2011 18:46, em um total de 1 vez.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por liviabgomes » Qua Jun 01, 2011 17:54
por liviabgomes » Qua Jun 01, 2011 17:54
qual das duas explicações aplica-se melhor a integral definida? a primeira ou a segunda?
-
liviabgomes
- Usuário Ativo

-
- Mensagens: 15
- Registrado em: Seg Mai 30, 2011 16:04
- Formação Escolar: GRADUAÇÃO
- Área/Curso: matemática licenciatura
- Andamento: cursando
 por liviabgomes » Qua Jun 01, 2011 17:58
por liviabgomes » Qua Jun 01, 2011 17:58
fiz pela segunda explicação e deu -1/3. está correto?
-
liviabgomes
- Usuário Ativo

-
- Mensagens: 15
- Registrado em: Seg Mai 30, 2011 16:04
- Formação Escolar: GRADUAÇÃO
- Área/Curso: matemática licenciatura
- Andamento: cursando
 por carlosalesouza » Qui Jun 02, 2011 08:53
por carlosalesouza » Qui Jun 02, 2011 08:53
Livia,
Certa está a resposta do Luiz... rs
Não teima com o Luiz...

Me ignora... hehehhee
Um abraço
Carlos Alexandre
Ciências Contábeis - FECEA/PR
Matemática - UEPG/PR
-
carlosalesouza
- Colaborador Voluntário

-
- Mensagens: 103
- Registrado em: Sex Abr 29, 2011 17:28
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática -LIC
- Andamento: cursando
 por carlosalesouza » Qui Jun 02, 2011 12:38
por carlosalesouza » Qui Jun 02, 2011 12:38
Hehehe...
Muito obrigado, Luiz,...
De fato, eu me perdi no acúmulo de procedimentos que fiz... rs e me perdi em alguns detalhes que comprometeram o resultado...
Um abraço
Carlos Alexandre
Ciências Contábeis - FECEA/PR
Matemática - UEPG/PR
-
carlosalesouza
- Colaborador Voluntário

-
- Mensagens: 103
- Registrado em: Sex Abr 29, 2011 17:28
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática -LIC
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Integral] Resolver Integral definida com trigonometria
por rodrigoboreli » Dom Set 07, 2014 01:02
- 1 Respostas
- 4342 Exibições
- Última mensagem por adauto martins

Sex Out 17, 2014 12:39
Cálculo: Limites, Derivadas e Integrais
-
- [Cálculo Integral] Integral Definida
por ARCS » Sáb Fev 02, 2013 21:37
- 2 Respostas
- 3671 Exibições
- Última mensagem por e8group

Sáb Fev 02, 2013 22:13
Cálculo: Limites, Derivadas e Integrais
-
- [integral] integral definida por partes
por gabriel feron » Seg Mar 11, 2013 00:48
- 2 Respostas
- 3064 Exibições
- Última mensagem por gabriel feron

Seg Mar 11, 2013 18:19
Cálculo: Limites, Derivadas e Integrais
-
- [Integral] Derivar integral definida
por troziinho » Ter Mar 31, 2015 20:26
- 0 Respostas
- 2498 Exibições
- Última mensagem por troziinho

Ter Mar 31, 2015 20:26
Cálculo: Limites, Derivadas e Integrais
-
- Integral definida
por exploit » Ter Set 07, 2010 19:17
- 4 Respostas
- 3620 Exibições
- Última mensagem por exploit

Qua Set 08, 2010 19:58
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 4 visitantes
Assunto:
Taxa de variação
Autor:
felipe_ad - Ter Jun 29, 2010 19:44
Como resolvo uma questao desse tipo:
Uma usina de britagem produz pó de pedra, que ao ser depositado no solo, forma uma pilha cônica onde a altura é aproximadamente igual a 4/3 do raio da base.
(a) Determinar a razão de variação do volume em relação ao raio da base.
(b) Se o raio da base varia a uma taxa de 20 cm/s, qual a razão de variação do volume quando o raio mede 2 m?
A letra (a) consegui resolver e cheguei no resultado correto de

Porem, nao consegui chegar a um resultado correto na letra (b). A resposta certa é

Alguem me ajuda? Agradeço desde já.
Assunto:
Taxa de variação
Autor:
Elcioschin - Qua Jun 30, 2010 20:47
V = (1/3)*pi*r²*h ----> h = 4r/3
V = (1/3)*pi*r²*(4r/3) ----> V = (4*pi/9)*r³
Derivando:
dV/dr = (4*pi/9)*(3r²) -----> dV/dr = 4pi*r²/3
Para dr = 20 cm/s = 0,2 m/s e R = 2 m ----> dV/0,2 = (4*pi*2²)/3 ----> dV = (3,2/3)*pi ----> dV ~= 1,066*pi m³/s
Assunto:
Taxa de variação
Autor:
Guill - Ter Fev 21, 2012 21:17
Temos que o volume é dado por:

Temos, portanto, o volume em função do raio. Podemos diferenciar implicitamente ambos os lados da equação em função do tempo, para encontrar as derivadas em função do tempo:

Sabendo que a taxa de variação do raio é 0,2 m/s e que queremos ataxa de variação do volume quando o raio for 2 m:


Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 sen(x) cos²(x) dx=
sen(x) cos²(x) dx=



![\\
sen(x).cos^2(x)\\
\left [sen(x).cos(x)\right ].cos(x)\\
\left [ \frac{1}{2}sen(2x)\right].cos(x)\\
\frac{1}{2}[sen(2x).cos(x)]\\
\frac{1}{2}\left[\frac{1}{2}(sen(x+2x)-sen(x-2x))\right ]\\
\frac{1}{4}[sen(3x)-sen(-x)]\\
\frac{1}{4}[sen(3x)+sen(x)] \\
sen(x).cos^2(x)\\
\left [sen(x).cos(x)\right ].cos(x)\\
\left [ \frac{1}{2}sen(2x)\right].cos(x)\\
\frac{1}{2}[sen(2x).cos(x)]\\
\frac{1}{2}\left[\frac{1}{2}(sen(x+2x)-sen(x-2x))\right ]\\
\frac{1}{4}[sen(3x)-sen(-x)]\\
\frac{1}{4}[sen(3x)+sen(x)]](/latexrender/pictures/a3553111601b4164756c1f342ca143a5.png)
![\\
\displaystyle \int_0^\frac{\pi}{2}[sen(3x)+sen(x)]dx \\
\displaystyle \int_0^\frac{\pi}{2}[sen(3x)+sen(x)]dx](/latexrender/pictures/552ebeee3f2d9e58580e76e20ea4868f.png)
![\\
\left [-cos(3x)-cos(x)\right ]_0^\frac{\pi}{2}\\
\left [-cos\left(3.\frac{\pi}{2}\right )-cos\left(\frac{\pi}{2}\right)\right ]-[-cos(3.0)-cos(0)]\\ \\
\left [-cos(3x)-cos(x)\right ]_0^\frac{\pi}{2}\\
\left [-cos\left(3.\frac{\pi}{2}\right )-cos\left(\frac{\pi}{2}\right)\right ]-[-cos(3.0)-cos(0)]\\](/latexrender/pictures/88d788c966f6b5ee276e788add593252.png)

![\\
\left [-(0)-(0)\right ]-\left [-(1)-(1)\right ]\\
0-(-2) = 2 \\
\left [-(0)-(0)\right ]-\left [-(1)-(1)\right ]\\
0-(-2) = 2](/latexrender/pictures/9ff3f3fe5b993d4ab4f3b3d746b34351.png)

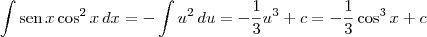 .
. , com
, com 
![\int_0^\frac{\pi}{2} \textrm{sen}\,x\cos^2 x \,dx = \left[- \frac{1}{3} \cos^3 x\right]_0^\frac{\pi}{2} = \left(- \frac{1}{3} \cos^3 \frac{\pi}{2}\right) - \left(- \frac{1}{3} \cos^3 0\right) = \frac{1}{3} \int_0^\frac{\pi}{2} \textrm{sen}\,x\cos^2 x \,dx = \left[- \frac{1}{3} \cos^3 x\right]_0^\frac{\pi}{2} = \left(- \frac{1}{3} \cos^3 \frac{\pi}{2}\right) - \left(- \frac{1}{3} \cos^3 0\right) = \frac{1}{3}](/latexrender/pictures/95a03fd0e7b6c22fbfc47108025bf29e.png)

![\int_0^\frac{\pi}{2} \textrm{sen}\,x\cos^2 x \,dx = \frac{1}{4}\int_0^\frac{\pi}{2}\textrm{sen}\,3x + \textrm{sen}\,x \,dx = \left[-\frac{1}{12}\cos 3x - \frac{1}{4}\cos x\right]_0^\frac{\pi}{2} \int_0^\frac{\pi}{2} \textrm{sen}\,x\cos^2 x \,dx = \frac{1}{4}\int_0^\frac{\pi}{2}\textrm{sen}\,3x + \textrm{sen}\,x \,dx = \left[-\frac{1}{12}\cos 3x - \frac{1}{4}\cos x\right]_0^\frac{\pi}{2}](/latexrender/pictures/705fc07dac52aa016f39f075a31a2f24.png)