 por Psilocybe » Ter Mai 31, 2011 20:33
por Psilocybe » Ter Mai 31, 2011 20:33
Tenho esse limite:

![\[\lim_{x\to 0+}{\left( \frac{\mathrm{sen}\left( x\right) }{x}\right) }^{x-1}\] \[\lim_{x\to 0+}{\left( \frac{\mathrm{sen}\left( x\right) }{x}\right) }^{x-1}\]](/latexrender/pictures/3ec758ae337ac00465a14558ba9e05de.png)
Chutei valores perto de 0+, e o limite resultou perto de 1. Será que ta certo? Isso significa que não deu indeterminação ? Não precisa aplicar nenhuma L'Hôpital ?
-
Psilocybe
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Seg Abr 04, 2011 09:17
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Ciência da Computação
- Andamento: cursando
 por Claudin » Ter Mai 31, 2011 21:20
por Claudin » Ter Mai 31, 2011 21:20
Cheguei no resultado 1 também
sem utilizar regra de l'Hopital
"O que sabemos é uma gota, o que não sabemos é um oceano." - Isaac Newton
-
Claudin
- Colaborador Voluntário

-
- Mensagens: 913
- Registrado em: Qui Mai 12, 2011 17:34
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por carlosalesouza » Qua Jun 01, 2011 00:27
por carlosalesouza » Qua Jun 01, 2011 00:27
Isso é um limite notável.... note que, quando x tende a 0, o expoente tende a -1... então a função tende a

Onde u = sen(x) e v = x... assim, o limite resulta em
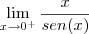
, que é um limite notável, igual a 1... logo, o limite lateral existe e é 1
Carlos Alexandre
Ciências Contábeis - FECEA/PR
Matemática - UEPG/PR
-
carlosalesouza
- Colaborador Voluntário

-
- Mensagens: 103
- Registrado em: Sex Abr 29, 2011 17:28
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática -LIC
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Mais um limite!
por flima » Sáb Ago 27, 2011 14:57
- 6 Respostas
- 2909 Exibições
- Última mensagem por LuizAquino

Dom Ago 28, 2011 11:36
Cálculo: Limites, Derivadas e Integrais
-
- Mais uma de sequência
por Molina » Dom Mai 03, 2009 06:07
- 4 Respostas
- 2902 Exibições
- Última mensagem por lucasguedes

Ter Jul 07, 2009 21:08
Desafios Difíceis
-
- MAIS UMA QUESTÃO DE G.A
por GABRIELA » Ter Set 29, 2009 18:57
- 3 Respostas
- 2543 Exibições
- Última mensagem por Elcioschin

Qua Set 30, 2009 20:54
Geometria Analítica
-
- Mais uma questão
por GABRIELA » Seg Dez 07, 2009 17:16
- 1 Respostas
- 2196 Exibições
- Última mensagem por Elcioschin

Seg Dez 07, 2009 19:23
Estatística
-
- Mais um desafio..
por victoreis1 » Seg Nov 22, 2010 21:26
- 3 Respostas
- 2523 Exibições
- Última mensagem por Molina

Seg Nov 22, 2010 23:54
Desafios Difíceis
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 10:38
Olá ! Tenho essa dúvida e não consigo montar o problema para resolução:
Qual é o racional não nulo cujo o quadrado é igual à sua terça parte ?
Grata.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 12:27

Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 12:55
também pensei que fosse assim, mas a resposta é

.
Obrigada Fantini.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 13:01

Como

:

O que você fez?
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 16:17
eu só consegui fazer a igualdade, não consegui desenvolver o restante, não pensei em fatoração, mas agora entendi o que vc fez.
Obrigada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.

![\[\lim_{x\to 0+}{\left( \frac{\mathrm{sen}\left( x\right) }{x}\right) }^{x-1}\] \[\lim_{x\to 0+}{\left( \frac{\mathrm{sen}\left( x\right) }{x}\right) }^{x-1}\]](/latexrender/pictures/3ec758ae337ac00465a14558ba9e05de.png)


![\[\lim_{x\to 0+}{\left( \frac{\mathrm{sen}\left( x\right) }{x}\right) }^{x-1}\] \[\lim_{x\to 0+}{\left( \frac{\mathrm{sen}\left( x\right) }{x}\right) }^{x-1}\]](/latexrender/pictures/3ec758ae337ac00465a14558ba9e05de.png)



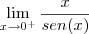 , que é um limite notável, igual a 1... logo, o limite lateral existe e é 1
, que é um limite notável, igual a 1... logo, o limite lateral existe e é 1

 .
.
 :
: