 por wallsoares » Ter Mai 31, 2011 19:33
por wallsoares » Ter Mai 31, 2011 19:33
Pessoal, impaquei total nesse exercicio, apenas fiz a troca da função e não consigo manipular os valores, alguem poderia me ajudar?
Obrigado
Questão: Encontre o valor de ' y ':
![g(x)=sinx+cosx,
y= [g(x/2) - g(2x)] / [ g(x/6) + g(0) ] g(x)=sinx+cosx,
y= [g(x/2) - g(2x)] / [ g(x/6) + g(0) ]](/latexrender/pictures/0cbac1579cac5e04cc34d983d1c2880b.png)
-
wallsoares
- Novo Usuário

-
- Mensagens: 7
- Registrado em: Seg Mar 21, 2011 19:48
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por Molina » Ter Mai 31, 2011 20:06
por Molina » Ter Mai 31, 2011 20:06
Boa noite, Wall.
Você precisa conhecer as principais identidades trigonométricas para começar a questão.

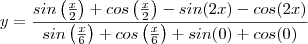
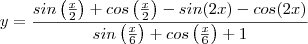
Agora esses termos podem ser calculados individualmente, através de identidades trigonométricas.

Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por wallsoares » Qua Jun 01, 2011 19:04
por wallsoares » Qua Jun 01, 2011 19:04
Diego, Muito obrigado pela atenção, porém foi exatamente nesse ponto em que eu empaquei quando criei o tópico =).
Será que não poderia dar mais um passinho apenas? Depois eu me viro.
Obrigado.
-
wallsoares
- Novo Usuário

-
- Mensagens: 7
- Registrado em: Seg Mar 21, 2011 19:48
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por Molina » Qua Jun 01, 2011 23:07
por Molina » Qua Jun 01, 2011 23:07
Boa noite.
wallsoares escreveu:Diego, Muito obrigado pela atenção, porém foi exatamente nesse ponto em que eu empaquei quando criei o tópico =).
Será que não poderia dar mais um passinho apenas? Depois eu me viro.
Obrigado.
Você precisa encontrar as
relações trigonométricas corretas para tentar eliminar alguns termos e melhorar a cada dessa equação.
A princípio eu não vi muitas melhoras, você tem o gabarito para conferir?
Pois, por exemplo, cos(2x) tem mais de uma forma de transformá-lo.
Obrigado!
Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por wallsoares » Qua Jun 01, 2011 23:16
por wallsoares » Qua Jun 01, 2011 23:16
Boa noite Diego,
Muito obrigado pela ajudam, só tinha que abrir mesmo o termo do cos 2x.
Agradeço pela atenção.
Abraço
-
wallsoares
- Novo Usuário

-
- Mensagens: 7
- Registrado em: Seg Mar 21, 2011 19:48
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
Voltar para Trigonometria
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Ajuda com exercicio!!!
por tuany » Seg Mar 24, 2008 15:34
- 3 Respostas
- 4118 Exibições
- Última mensagem por tuany

Ter Mar 25, 2008 16:50
Funções
-
- Ajuda com exercicio!!!
por karol_agnelli » Qua Mar 26, 2008 19:40
- 6 Respostas
- 7284 Exibições
- Última mensagem por Cleyson007

Qua Jun 10, 2009 15:23
Tópicos sem Interação (leia as regras)
-
- ajuda com o exercicio
por Mimizinha » Seg Mar 31, 2008 18:19
- 2 Respostas
- 3498 Exibições
- Última mensagem por Mimizinha

Ter Abr 01, 2008 10:24
Geometria Plana
-
- Ajuda em Exercício.
 por Levi23 » Dom Set 28, 2008 02:01
por Levi23 » Dom Set 28, 2008 02:01
- 12 Respostas
- 8852 Exibições
- Última mensagem por admin

Sáb Out 04, 2008 13:51
Trigonometria
-
- ajuda em exercicio
por anabela » Qua Nov 25, 2009 15:31
- 2 Respostas
- 3131 Exibições
- Última mensagem por anabatista

Ter Abr 09, 2013 00:10
Estatística para Licenciatura I
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 10:38
Olá ! Tenho essa dúvida e não consigo montar o problema para resolução:
Qual é o racional não nulo cujo o quadrado é igual à sua terça parte ?
Grata.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 12:27

Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 12:55
também pensei que fosse assim, mas a resposta é

.
Obrigada Fantini.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 13:01

Como

:

O que você fez?
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 16:17
eu só consegui fazer a igualdade, não consegui desenvolver o restante, não pensei em fatoração, mas agora entendi o que vc fez.
Obrigada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![g(x)=sinx+cosx,
y= [g(x/2) - g(2x)] / [ g(x/6) + g(0) ] g(x)=sinx+cosx,
y= [g(x/2) - g(2x)] / [ g(x/6) + g(0) ]](/latexrender/pictures/0cbac1579cac5e04cc34d983d1c2880b.png)

![g(x)=sinx+cosx,
y= [g(x/2) - g(2x)] / [ g(x/6) + g(0) ] g(x)=sinx+cosx,
y= [g(x/2) - g(2x)] / [ g(x/6) + g(0) ]](/latexrender/pictures/0cbac1579cac5e04cc34d983d1c2880b.png)


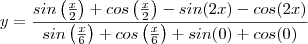
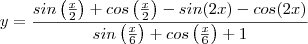






 .
.
 :
: