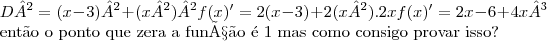por elbert005 » Ter Mai 31, 2011 15:41
por elbert005 » Ter Mai 31, 2011 15:41
Olá amigos,
Estou com um grande problema para resolução de uma atividade na qual precisarei apresentar amanhã na aula de cálculo.
O problema é o seguinte:
Encontre o ponto P na parábola y=x² que está mais próximo de (3,0) . Justifique sua resposta que o ponto que você encontrou é realmente o mais próximo.
Para resolver eu isolei x e estou trabalhando em termos de y, mais consigo chegar na resposta (1,1). Mas não acho uma maneira de provar essa reposta.
Preciso de ajuda!!!
Elbert
-
elbert005
- Novo Usuário

-
- Mensagens: 4
- Registrado em: Ter Mai 31, 2011 15:20
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Mecânica
- Andamento: cursando
 por LuizAquino » Ter Mai 31, 2011 17:23
por LuizAquino » Ter Mai 31, 2011 17:23
Em exercícios de otimização você precisa primeiro obter a função que deseja otimizar. Em boa parte dos exercícios a função não é fornecida diretamente.
Pois bem, perceba que todos os pontos sobre a parábola y = x² têm o formato (k, k²), para algum real k.
Agora, basta armar a função que fornece a distância desse ponto ao ponto (3, 0).
Vale lembrar que dos conhecimentos de Geometria Analítica sabemos que a distância do ponto P = (x0, y0) à Q = (x1, y1) é dada por:

.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por elbert005 » Ter Mai 31, 2011 17:48
por elbert005 » Ter Mai 31, 2011 17:48
Boa tarde Luiz,
Eu tenho a seguinte dúvida:
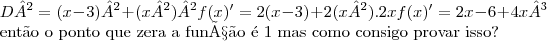
-
elbert005
- Novo Usuário

-
- Mensagens: 4
- Registrado em: Ter Mai 31, 2011 15:20
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Mecânica
- Andamento: cursando
 por elbert005 » Ter Mai 31, 2011 17:50
por elbert005 » Ter Mai 31, 2011 17:50
consequentemente a imagem em y= 1² = 1
??????
seria um teste da segunda derivada???
-
elbert005
- Novo Usuário

-
- Mensagens: 4
- Registrado em: Ter Mai 31, 2011 15:20
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Mecânica
- Andamento: cursando
 por LuizAquino » Ter Mai 31, 2011 18:08
por LuizAquino » Ter Mai 31, 2011 18:08
D² = (x - 3)² +(x²)²
f'(x) = 2(x-3) + 2(x²).2x
f(x)' = 2x - 6 + 4x³
então o ponto que zera a função é 1 mas como consigo provar isso?
Ora, se você quer comprovar que x = c é raiz da função f(x), então basta você exibir que f(c) = 0. Mas, se você quer explicar como obteve que x = c é uma raiz, aí é outra história. No caso desse exercício, como temos uma equação polinomial, você poderia usar o
Teorema das Raízes Racionais.
Vale lembrar que para concluir que (1, f(1)) é o ponto de mínimo você ainda deve calcular a segunda derivada e verificar se f''(1) > 0.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Otimizacao
por Taisa » Sex Nov 12, 2010 13:53
- 1 Respostas
- 2143 Exibições
- Última mensagem por MarceloFantini

Sex Nov 12, 2010 14:36
Cálculo: Limites, Derivadas e Integrais
-
- Otimização
 por AlbertoAM » Sáb Mai 14, 2011 21:36
por AlbertoAM » Sáb Mai 14, 2011 21:36
- 4 Respostas
- 2483 Exibições
- Última mensagem por AlbertoAM

Dom Mai 15, 2011 19:23
Cálculo: Limites, Derivadas e Integrais
-
- Otimizacao !!!!!!
 por andersoneng » Qua Jun 27, 2012 12:26
por andersoneng » Qua Jun 27, 2012 12:26
- 7 Respostas
- 5267 Exibições
- Última mensagem por andersoneng

Qui Jun 28, 2012 10:24
Cálculo: Limites, Derivadas e Integrais
-
- Otimização
por Jhonata » Seg Fev 25, 2013 19:24
- 1 Respostas
- 1407 Exibições
- Última mensagem por Russman

Seg Fev 25, 2013 20:28
Cálculo: Limites, Derivadas e Integrais
-
- oTIMIZAÇÃO
por Pinheiro Rosa Victor » Qui Mai 02, 2013 11:11
- 0 Respostas
- 1252 Exibições
- Última mensagem por Pinheiro Rosa Victor

Qui Mai 02, 2013 11:11
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 3 visitantes
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


 .
.