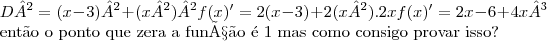Olá amigos,
Estou com um grande problema para resolução de uma atividade na qual precisarei apresentar amanhã na aula de cálculo.
O problema é o seguinte:
Encontre o ponto P na parábola y=x² que está mais próximo de (3,0) . Justifique sua resposta que o ponto que você encontrou é realmente o mais próximo.
Para resolver eu isolei x e estou trabalhando em termos de y, mais consigo chegar na resposta (1,1). Mas não acho uma maneira de provar essa reposta.
Preciso de ajuda!!!
Elbert


 .
.