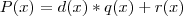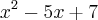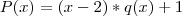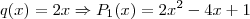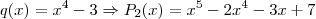por maykonnunes » Seg Mai 30, 2011 23:00
por maykonnunes » Seg Mai 30, 2011 23:00
Classifique cada afirmação a seguir em Verdadeira ou Falsa, justifique
a) Existe apenas um polinômio que dividido por x-2 ou por x-3 dá resto 1.
b) Não existe polinômio algum que dividido por x-2 ou por x-3 dá resto 1.
c) Exsite uma infinidade de polinômio que dividido por x-2 ou por x-3 dá resto 1.
aguardo ajuda
Abraços
-
maykonnunes
- Usuário Ativo

-
- Mensagens: 16
- Registrado em: Qua Abr 27, 2011 02:35
- Formação Escolar: GRADUAÇÃO
- Área/Curso: matematica
- Andamento: cursando
 por Molina » Ter Mai 31, 2011 02:37
por Molina » Ter Mai 31, 2011 02:37
Boa noite.
Lembre-se que:
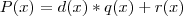
onde,
P(x) = Dividendo;
d(x) = Divisor;
q(x) = Quociente;
r(x) = Resto.
Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por maykonnunes » Ter Mai 31, 2011 22:35
por maykonnunes » Ter Mai 31, 2011 22:35
Não sei se entendi seu raciocinio para a solução
P(x)=(x-2)*q(X)+1
p(X)=(X-3)*Q(X)+1
OU PENSEI EM...
p(X)=(X-2)(X-3)+R
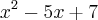
so não sei como mostrar se le é unico ou não
-
maykonnunes
- Usuário Ativo

-
- Mensagens: 16
- Registrado em: Qua Abr 27, 2011 02:35
- Formação Escolar: GRADUAÇÃO
- Área/Curso: matematica
- Andamento: cursando
 por Molina » Qui Jun 02, 2011 01:24
por Molina » Qui Jun 02, 2011 01:24
Boa noite, Maycon.
Desculpe a demora...
Duas alternativas se anulam quando se é mostrado que uma delas é verdade. Ou seja, só temos uma verdadeira.
Perceba que a questão quer saber se há (ou não) polinômio que dividido por (x-2)
OU (x-3) deixa resto 1.
Como eu disse anteriormente:
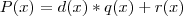
Queremos encontrar (ou não) P(x)'s... Encontraremos um, vários ou nenhum. Vejamos:
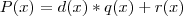
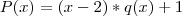
Perceba que dependendo do q(x) que eu escolher, conseguirei um polinômio P(x) que quando dividido por (x-2) deixa resto 1, exemplos:
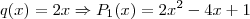
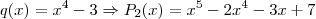
etc.
O mesmo pode ser feito para descobrir polinômios que divididos por (x-3) deixam resto 1.
Ou seja, há infinitas soluções.

Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por maykonnunes » Sex Jun 10, 2011 15:15
por maykonnunes » Sex Jun 10, 2011 15:15
agradeço atenção
desde já peço desculpa, mas não encontrei uma forma (um local onde pudesse mandar uma mensagem pessoal para você), em que fase vcoê está? também sou aluno da UFSC aluno EAD, quero saber se voce tem algum material de geometria III, que possa ajudar nesta matéria; Abraços e mais uma vez desculpa usar aqui.
-
maykonnunes
- Usuário Ativo

-
- Mensagens: 16
- Registrado em: Qua Abr 27, 2011 02:35
- Formação Escolar: GRADUAÇÃO
- Área/Curso: matematica
- Andamento: cursando
Voltar para Polinômios
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Classificar condições
 por roninhasmr » Seg Nov 13, 2017 14:31
por roninhasmr » Seg Nov 13, 2017 14:31
- 0 Respostas
- 2348 Exibições
- Última mensagem por roninhasmr

Seg Nov 13, 2017 14:31
Lógica
-
- ufsm-se cada ratazana
por Natalie » Sex Set 16, 2011 17:28
- 3 Respostas
- 3396 Exibições
- Última mensagem por MarceloFantini

Sex Set 16, 2011 18:15
Progressões
-
- Formula Somatorio de cada Termo
por carlosecc » Seg Nov 19, 2012 21:55
- 2 Respostas
- 2583 Exibições
- Última mensagem por carlosecc

Ter Nov 20, 2012 20:41
Sequências
-
- Bala para cada neto
por andersonsouza » Seg Fev 11, 2013 16:01
- 4 Respostas
- 3054 Exibições
- Última mensagem por andersonsouza

Seg Fev 11, 2013 23:24
Aritmética
-
- para cada vetor V o simétrico -V é único
por dkiwilson » Sáb Set 23, 2017 19:16
- 0 Respostas
- 2590 Exibições
- Última mensagem por dkiwilson

Sáb Set 23, 2017 19:16
Álgebra Linear
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.