fórmula: L= ?{1+ [f '(x)]^2)}^(1/2)*dx
ou:
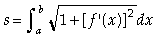
podem me ajudar? brigada.

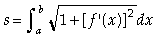




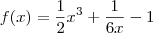 .
. .
.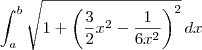 .
. .
.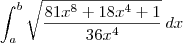 .
.


liviabgomes escreveu:(...) eu derivo com a raiz? ou tiro a raiz?
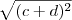 (com c + d positivo), então você pode simplificar ficando com (c + d) . Ou seja, você usará a propriedade
(com c + d positivo), então você pode simplificar ficando com (c + d) . Ou seja, você usará a propriedade 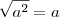 (desde que a seja positivo). Caso não seja possível, aí você deverá usar alguma técnica específica. Às vezes, por exemplo, usamos substituições trigonométricas.
(desde que a seja positivo). Caso não seja possível, aí você deverá usar alguma técnica específica. Às vezes, por exemplo, usamos substituições trigonométricas.

 , com x > -3.
, com x > -3.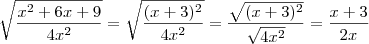 .
.
 muito obrigada pela ajuuda! Tuas explicações me fizeram enxergar de outra maneira a questão.
muito obrigada pela ajuuda! Tuas explicações me fizeram enxergar de outra maneira a questão.
Voltar para Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 5 visitantes
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png) (dica : igualar a expressão a
(dica : igualar a expressão a  e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)