 por -civil- » Seg Mai 30, 2011 20:31
por -civil- » Seg Mai 30, 2011 20:31
Estou tentando resolver os exercícios de esboço de gráfico do capítulo 9 do Guidorizzi. Para conseguir esboçar o gráfico, o primeiro passo é encontrar as raízes da função.
Mas como eu calculo as raízes dessas funções cúbicas?
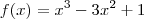
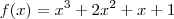
Tentei substituir por alguns números (sem êxito), mas acho que esse não é o melhor método.
-
-civil-
- Usuário Dedicado

-
- Mensagens: 47
- Registrado em: Sex Abr 22, 2011 12:31
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Civil
- Andamento: cursando
 por Claudin » Seg Mai 30, 2011 20:38
por Claudin » Seg Mai 30, 2011 20:38
Faz pesquisa de raízes!
"O que sabemos é uma gota, o que não sabemos é um oceano." - Isaac Newton
-
Claudin
- Colaborador Voluntário

-
- Mensagens: 913
- Registrado em: Qui Mai 12, 2011 17:34
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por LuizAquino » Seg Mai 30, 2011 20:56
por LuizAquino » Seg Mai 30, 2011 20:56
Na verdade, você vai precisar calcular as raízes da equação f'(x) = 0 e f''(x) = 0.
Para ambas as funções do exercício, note que a primeira equação será polinomial do 2° grau. Já a segunda equação será polinomial do 1º grau.
SugestãoPara saber como resolver equações polinomiais de 3° grau genéricas, procure pelo método de Cardano. Leia mais a respeito:
Equação cúbicahttp://pt.wikipedia.org/wiki/Equa%C3%A7 ... %C3%BAbica
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por -civil- » Seg Mai 30, 2011 21:20
por -civil- » Seg Mai 30, 2011 21:20
As raízes de
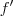
e
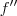
eu consegui encontrar. Vou ler sobre esse método de Cardano e ver se eu consigo encontrar as raízes. Uma solução alternativa que eu encontrei foi considerar três raízes dentro de três intervalos diferentes. No caso de
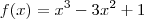
, considerei que as raízes são a, b, c e que
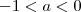
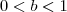
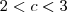
Daí,

é negativa em ]

, a] e em [b, c]
e

é positiva em [a,b] e em [c,

[
-
-civil-
- Usuário Dedicado

-
- Mensagens: 47
- Registrado em: Sex Abr 22, 2011 12:31
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Civil
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Divisão de polinômios
por manuoliveira » Dom Nov 14, 2010 14:00
- 1 Respostas
- 2594 Exibições
- Última mensagem por VtinxD

Seg Nov 15, 2010 01:13
Polinômios
-
- divisão de polinomios
por theSinister » Seg Mai 23, 2011 17:11
- 6 Respostas
- 3905 Exibições
- Última mensagem por theSinister

Seg Mai 23, 2011 22:34
Álgebra Elementar
-
- Divisão de Polinômios
por Claudin » Qua Ago 03, 2011 20:25
- 3 Respostas
- 2184 Exibições
- Última mensagem por Claudin

Qui Ago 04, 2011 15:46
Polinômios
-
- Divisão de polinômios
por Gaules » Qua Out 19, 2011 16:47
- 0 Respostas
- 1415 Exibições
- Última mensagem por Gaules

Qua Out 19, 2011 16:47
Polinômios
-
- Divisão de polinômios
por Pri Ferreira » Ter Mai 08, 2012 21:28
- 1 Respostas
- 1398 Exibições
- Última mensagem por DanielFerreira

Ter Mai 08, 2012 23:02
Polinômios
Usuários navegando neste fórum: Nenhum usuário registrado e 5 visitantes
Assunto:
(FGV) ... função novamente rs
Autor:
my2009 - Qua Dez 08, 2010 21:48
Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
Assunto:
(FGV) ... função novamente rs
Autor: Anonymous - Qui Dez 09, 2010 17:25
Uma função de 1º grau é dada por

.
Temos que para

,

e para

,

.

Ache o valor de

e

, monte a função e substitua

por

.
Assunto:
(FGV) ... função novamente rs
Autor:
Pinho - Qui Dez 16, 2010 13:57
my2009 escreveu:Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
f(x)= 2.x
f(3)=2.3=6
f(4)=2.4=8
f(10)=2.10=20
Assunto:
(FGV) ... função novamente rs
Autor:
dagoth - Sex Dez 17, 2010 11:55
isso ai foi uma questao da FGV?
haahua to precisando trocar de faculdade.
Assunto:
(FGV) ... função novamente rs
Autor:
Thiago 86 - Qua Mar 06, 2013 23:11
Saudações!

ví suaquestão e tentei resolver, depois você conta-me se eu acertei.
Uma função de 1º grau é dada por y=3a+b
Resposta :
3a+b=6 x(4)
4a+b=8 x(-3)
12a+4b=24
-12a-3b=-24
b=0
substituindo b na 1°, ttenho que: 3a+b=6
3a+0=6
a=2
substituindo em: y=3a+b
y=30+0
y=30

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
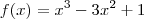
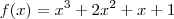

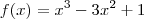
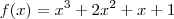



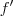 e
e 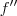 eu consegui encontrar. Vou ler sobre esse método de Cardano e ver se eu consigo encontrar as raízes. Uma solução alternativa que eu encontrei foi considerar três raízes dentro de três intervalos diferentes. No caso de
eu consegui encontrar. Vou ler sobre esse método de Cardano e ver se eu consigo encontrar as raízes. Uma solução alternativa que eu encontrei foi considerar três raízes dentro de três intervalos diferentes. No caso de 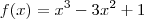 , considerei que as raízes são a, b, c e que
, considerei que as raízes são a, b, c e que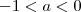
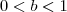
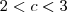
 é negativa em ]
é negativa em ] , a] e em [b, c]
, a] e em [b, c] é positiva em [a,b] e em [c,
é positiva em [a,b] e em [c,  [
[
 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.
