Determine a probabilidade de sair o número 5 em 2 lançamentos sucessivos de um dado.
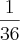
Sorteando um número de 1 a 30, qual a probabilidade de que ele seja par ou múltiplo de 3.

No jogo da sena seies números distintos são sorteados dentre os números 1, 2, ...,50. A probabilidade de que uma extração, os seis números sorteados sejam ímpares.
1,12%
Qual a probabilidade de, no lançamento simultâneo de dois dados diferentes, obter-mos soma 7?

Na escolha de um número de 1 a 30, qual a probabilidade de que seja sorteado um múltiplo de 5?

Considerando o experimento sorteio de um número de 1 a 20, determinar o evento para obter 1 número:
a-) múltiplo de 3

b-) Primo
 (essa errei, porque esqueci de contar o 2 como primo! =/)
(essa errei, porque esqueci de contar o 2 como primo! =/)Calcule o termo independente de x no desenvolvimento de
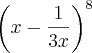 .
.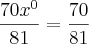
Determinar o coeficiente
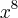 no desenvolvimento de
no desenvolvimento de ![{\left[2x + ( x - 1)² \right]}^{9} {\left[2x + ( x - 1)² \right]}^{9}](/latexrender/pictures/8907086776ef5f954fdaba3e54f29060.png) .
.126
Determinar o 4º termo no desenvolvimento de
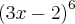 segundo os expoentes decrescentes de x.
segundo os expoentes decrescentes de x.{T}_{4} = -4320 x³
Determinar X, tal que
 .
.X= -1 e x=0, porém somente x=0, satisfaz as condições.



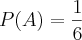
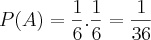


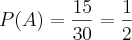


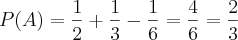
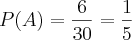
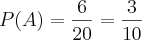
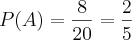

 .
.



