 por Giles » Sex Nov 07, 2008 09:06
por Giles » Sex Nov 07, 2008 09:06
Queria que corrigessem minha prova! =]
Determine a probabilidade de sair o número 5 em 2 lançamentos sucessivos de um dado.
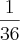
Sorteando um número de 1 a 30, qual a probabilidade de que ele seja par ou múltiplo de 3.

No jogo da sena seies números distintos são sorteados dentre os números 1, 2, ...,50. A probabilidade de que uma extração, os seis números sorteados sejam ímpares.
1,12%Qual a probabilidade de, no lançamento simultâneo de dois dados diferentes, obter-mos soma 7?

Na escolha de um número de 1 a 30, qual a probabilidade de que seja sorteado um múltiplo de 5?

Considerando o experimento sorteio de um número de 1 a 20, determinar o evento para obter 1 número:
a-) múltiplo de 3

b-) Primo

(essa errei, porque esqueci de contar o 2 como primo! =/)
Calcule o termo independente de x no desenvolvimento de
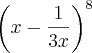
.
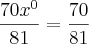
Determinar o coeficiente
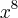
no desenvolvimento de
![{\left[2x + ( x - 1)² \right]}^{9} {\left[2x + ( x - 1)² \right]}^{9}](/latexrender/pictures/8907086776ef5f954fdaba3e54f29060.png)
.
126Determinar o 4º termo no desenvolvimento de
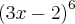
segundo os expoentes decrescentes de x.
{T}_{4} = -4320 x³Determinar X, tal que

.
X= -1 e x=0, porém somente x=0, satisfaz as condições. "As pessoas que vencem nessa vida são aquelas que procuram as circunstâncias de que precisam e quando não as encontram, as criam"
-

Giles
- Usuário Ativo

-
- Mensagens: 17
- Registrado em: Dom Out 19, 2008 11:14
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Curso Técnico em Construção Civil Integr
- Andamento: cursando
 por Molina » Sex Nov 07, 2008 16:39
por Molina » Sex Nov 07, 2008 16:39
Giles escreveu:Queria que corrigessem minha prova! =]
Determine a probabilidade de sair o número 5 em 2 lançamentos sucessivos de um dado.
Você pode tratar a possibilidade com a seguinte expressão:

Sendo assim os casos favoráveis é o número 5 que você quer conseguir, ou seja, há apenas 1 possibilidade. Os casos possíveis são todos os resultados do dado que poderia acontecer, ou seja, 6 possibilidades:
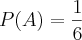
Como você vai fazer dois lançamentos sucessivos, multiplica-se essas possibilidades de casa lançamento:
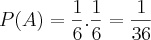
Bom estudo!

Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por Molina » Sex Nov 07, 2008 16:56
por Molina » Sex Nov 07, 2008 16:56
Giles escreveu:Queria que corrigessem minha prova! =]
Sorteando um número de 1 a 30, qual a probabilidade de que ele seja par ou múltiplo de 3.
Seguindo a mesma idéia do exercício anterior, vamos pegar os resultados que desejamos e dividir pelos resultados possíveis:
Par:
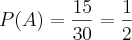
Múltiplo de 3:

Par e Múltiplo de 3:

Agora você faz as operações somando os pares com os multiplos de 3 e subtraindo as opções em que houve repetições (6, 12, 18, 24 e 30 - já que são pares e múltiplos de 3):
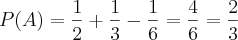
Bom estudo!

Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por Molina » Sex Nov 07, 2008 17:15
por Molina » Sex Nov 07, 2008 17:15
Giles escreveu:Queria que corrigessem minha prova! =]
Qual a probabilidade de, no lançamento simultâneo de dois dados diferentes, obter-mos soma 7?
Para a soma ser 7 há as seguintes possibilidades:
1 + 6 = 7
2 + 5 = 7
3 + 4 = 7
4 + 3 = 7
5 + 2 = 7
6 + 1 = 7
Vou tentar fazer essa sem a ajuda da fórmula. Seria assim:
Joguei o primeiro dado e vamos dizer que tenha caído no número 1. Para eu conseguir dar a soma igual a 7, ele precisa cair no 6, ou seja, tem uma possibilidade em seis possíveis:

E isso acontecerá com todos os outros números tambem, sempre jogando o primero dado, vai ter

de possibilidades do segundo cair pra soma dar 7.
Por isso concordo com a sua resposta de

Abraços!

Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por Molina » Sex Nov 07, 2008 17:18
por Molina » Sex Nov 07, 2008 17:18
Giles escreveu:Queria que corrigessem minha prova! =]
Na escolha de um número de 1 a 30, qual a probabilidade de que seja sorteado um múltiplo de 5?
Vamo seguir o mesmo pensamento, esta é tranquila:
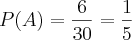
Abraços

Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por Molina » Sex Nov 07, 2008 17:25
por Molina » Sex Nov 07, 2008 17:25
Giles escreveu:Queria que corrigessem minha prova! =]
Considerando o experimento sorteio de um número de 1 a 20, determinar o evento para obter 1 número:
a-) múltiplo de 3

b-) Primo

a)
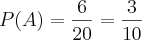
b) Entre 1 e 20 há oito números primos (2, 3, 5, 7, 11, 13, 17 e 19), logo:
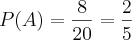
Abraços!

Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por Giles » Sex Nov 07, 2008 19:48
por Giles » Sex Nov 07, 2008 19:48
Desculpem-me a minha distração... Coloquei as questões de Binômio de Newton juntas! =/ Vou postar no lugar certo!
"As pessoas que vencem nessa vida são aquelas que procuram as circunstâncias de que precisam e quando não as encontram, as criam"
-

Giles
- Usuário Ativo

-
- Mensagens: 17
- Registrado em: Dom Out 19, 2008 11:14
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Curso Técnico em Construção Civil Integr
- Andamento: cursando
Voltar para Estatística
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Alguem pode ajudar-me?
por carlos r m oliveira » Seg Out 05, 2009 11:35
- 1 Respostas
- 2542 Exibições
- Última mensagem por Neperiano

Dom Jul 03, 2011 21:05
Estatística
-
- Alguém pode me ajudar?
por apoliveirarj » Seg Jul 19, 2010 18:20
- 1 Respostas
- 3390 Exibições
- Última mensagem por Douglasm

Seg Jul 19, 2010 18:49
Matemática Financeira
-
- Tem alguem que pode me ajuadr??
por Paulo A G » Sáb Abr 09, 2011 13:54
- 2 Respostas
- 1705 Exibições
- Última mensagem por Rogerio Murcila

Qua Mai 11, 2011 13:39
Matemática Financeira
-
- Alguém pode me ajudar?
por Andromeda » Seg Set 19, 2011 20:19
- 2 Respostas
- 2412 Exibições
- Última mensagem por Andromeda

Seg Set 19, 2011 21:13
Trigonometria
-
- lim x^2.sin(x/1), x=0. Alguém pode me ajudar?
por Arthur_Bulcao » Seg Abr 09, 2012 18:05
- 2 Respostas
- 2007 Exibições
- Última mensagem por fraol

Seg Abr 09, 2012 19:24
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
método de contagem
Autor:
sinuca147 - Seg Mai 25, 2009 09:10
Veja este exercício:
Se A = {

} e B = {

}, então o número de elementos A

B é:
Eu tentei resolver este exercício e achei a resposta "três", mas surgiram muitas dúvidas aqui durante a resolução.
Para determinar os elementos do conjunto A, eu tive de basicamente fazer um lista de vinte dividido por todos os números naturais maiores que zero e menores que vinte e um, finalmente identificando como elementos do conjunto A os números 1, 2, 4, 5, 10 e 20. Acho que procedi de maneira correta, mas fiquei pensando aqui se não existiria um método mais "sofisticado" e prático para que eu pudesse identificar ou ao menos contar o número de elementos do conjunto A, existe?
No processo de determinação dos elementos do conjunto B o que achei foi basicamente os múltiplos de cinco e seus opostos, daí me surgiram estas dúvidas:
existe oposto de zero?
existe inverso de zero?
zero é par, certo?
sendo x um número natural, -x é múltiplo de x?
sendo z um número inteiro negativo, z é múltiplo de z?
sendo z um número inteiro negativo, -z é múltiplo de z?
A resposta é 3?
Obrigado.
Assunto:
método de contagem
Autor:
Molina - Seg Mai 25, 2009 20:42
Boa noite, sinuca.
Se A = {

} você concorda que n só pode ser de 1 a 20? Já que pertence aos naturais?
Ou seja, quais são os divisores de 20? Eles são seis: 1, 2, 4, 5, 10 e 20.
Logo, o conjunto A é
A = {1, 2, 4, 5, 10, 20}
Se B = {

} você concorda que x será os múltiplos de 5 (positivos e negativos)? Já que m pertence ao conjunto Z?
Logo, o conjunto B é
B = {... , -25, -20, -15, -10, -5, 0, 5, 10, 15, 20, 25, ...
Feito isso precisamos ver os números que está em ambos os conjuntos, que são:
5, 10 e 20 (3 valores, como você achou).
Vou responder rapidamente suas dúvidas porque meu tempo está estourando. Qualquer dúvida, coloque aqui, ok?
sinuca147 escreveu:No processo de determinação dos elementos do conjunto B o que achei foi basicamente os múltiplos de cinco e seus opostos, daí me surgiram estas dúvidas:
existe oposto de zero? sim, é o próprio zero
existe inverso de zero? não, pois não há nenhum número que multiplicado por zero resulte em 1
zero é par, certo? sim, pois pode ser escrito da forma de 2n, onde n pertence aos inteiros
sendo x um número natural, -x é múltiplo de x? Sim, pois basta pegar x e multiplicar por -1 que encontramos -x
sendo z um número inteiro negativo, z é múltiplo de z? Sim, tais perguntando se todo número é multiplo de si mesmo
sendo z um número inteiro negativo, -z é múltiplo de z? Sim, pois basta pegar -z e multiplicar por -1 que encontramos x
A resposta é 3? Sim, pelo menos foi o que vimos a cima
Bom estudo,

Assunto:
método de contagem
Autor:
sinuca147 - Seg Mai 25, 2009 23:35
Obrigado, mas olha só este link
http://www.colegioweb.com.br/matematica ... ro-natural
neste link encontra-se a a frase:
Múltiplo de um número natural é qualquer número que possa ser obtido multiplicando o número natural por 0, 1, 2, 3, 4, 5, etc.
Para determinarmos os múltiplos de 15, por exemplo, devemos multiplicá-lo pela sucessão dos números naturais:
Ou seja, de acordo com este link -5 não poderia ser múltiplo de 5, assim como 5 não poderia ser múltiplo de -5, eu sempre achei que não interessava o sinal na questão dos múltiplos, assim como você me confirmou, mas e essa informação contrária deste site, tem alguma credibilidade?
Há e claro, a coisa mais bacana você esqueceu, quero saber se existe algum método de contagem diferente do manual neste caso:
Para determinar os elementos do conjunto A, eu tive de basicamente fazer um lista de vinte dividido por todos os números naturais maiores que zero e menores que vinte e um, finalmente identificando como elementos do conjunto A os números 1, 2, 4, 5, 10 e 20. Acho que procedi de maneira correta, mas fiquei pensando aqui se não existiria um método mais "sofisticado" e prático para que eu pudesse identificar ou ao menos contar o número de elementos do conjunto A, existe?
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
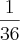




 (essa errei, porque esqueci de contar o 2 como primo! =/)
(essa errei, porque esqueci de contar o 2 como primo! =/)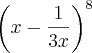 .
.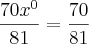
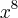 no desenvolvimento de
no desenvolvimento de ![{\left[2x + ( x - 1)² \right]}^{9} {\left[2x + ( x - 1)² \right]}^{9}](/latexrender/pictures/8907086776ef5f954fdaba3e54f29060.png) .
. segundo os expoentes decrescentes de x.
segundo os expoentes decrescentes de x. .
.


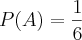
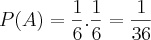


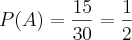


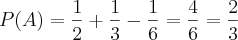
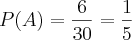
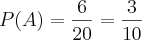
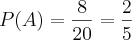
 } e B = {
} e B = { }, então o número de elementos A
}, então o número de elementos A  B é:
B é: