 por Nandodtx » Dom Mai 29, 2011 00:17
por Nandodtx » Dom Mai 29, 2011 00:17
Gente tenho que resolver o seguinte problema:
Um cocho no caso seria isso :
http://www.concrelaje.com.br/imgs/479d7 ... b5efd1.jpgEntao ele ta querendo a inclinação que fornece a maior area do trapezio. Já tentei colocar o valor da base maior e da altura em função do seno do angulo e a/3 mas a função fica mto grande e a derivada mais ainda.
Se alguem tiver alguma dica deixa ai! ^^
Editado pela última vez por
Nandodtx em Dom Mai 29, 2011 14:46, em um total de 1 vez.
-
Nandodtx
- Novo Usuário

-
- Mensagens: 6
- Registrado em: Sáb Mai 28, 2011 23:51
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Eng. Automação e Controle de processos
- Andamento: cursando
 por LuizAquino » Dom Mai 29, 2011 09:42
por LuizAquino » Dom Mai 29, 2011 09:42
A figura abaixo ilustra o exercício.
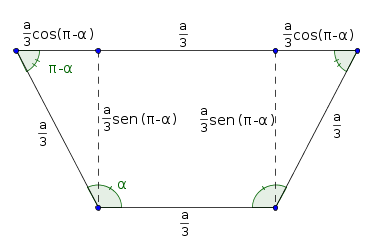
- trapézio.png (8.21 KiB) Exibido 6841 vezes
Você construiu uma figura semelhante?
Note que agora basta montar a função que fornece a área do trapézio em função do ângulo alfa. Vale lembrar que a incógnita
a será uma constante nesse contexto.
Além disso, eu gostaria de frisar que alguns exercícios são naturalmente trabalhosos. Nos problemas de otimização não podemos nos "assustar" com a função ou suas derivadas.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por Nandodtx » Dom Mai 29, 2011 10:12
por Nandodtx » Dom Mai 29, 2011 10:12
Então, a função eu conseguir fazer, mas o problema é que de alguma maneira eu to aplicando a regra da cadeia de forma errada. Não sei se deriva primeiro o produto e depois multiplica pela derivada do seno e do cosseno, ou deriva o sen e cos logo e depois aplica a regra pra produto de derivadas. :S
Editado pela última vez por
Nandodtx em Dom Mai 29, 2011 10:45, em um total de 2 vezes.
-
Nandodtx
- Novo Usuário

-
- Mensagens: 6
- Registrado em: Sáb Mai 28, 2011 23:51
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Eng. Automação e Controle de processos
- Andamento: cursando
 por LuizAquino » Dom Mai 29, 2011 10:40
por LuizAquino » Dom Mai 29, 2011 10:40
A função para a área terá mais ou menos o formato:
A(x) = f(g(x))h(g(x)).
Desse modo, temos que:
A'(x) = [f(g(x))h(g(x))]' = [f(g(x))]'h(g(x)) + f(g(x))[h(g(x))]' = f'(g(x))g'(x)h(g(x)) + f(g(x))h'(g(x))g'(x).
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por Nandodtx » Dom Mai 29, 2011 10:52
por Nandodtx » Dom Mai 29, 2011 10:52
A função fica assim:
![y = 2a^2 [sen(Pi - a).cos(Pi - a) + sen(Pi - a)] /9 y = 2a^2 [sen(Pi - a).cos(Pi - a) + sen(Pi - a)] /9](/latexrender/pictures/9a3980c85bb3ac53b51b6f2a657f22c9.png)
Então a derivada seria o primeiro termo derivado multiplicado pelo segundo termo normal e vice-versa no prox, mas dai, no segundo termo fica a derivada de
![[sen(Pi - a).cos(Pi - a) + sen(Pi - a)] ' [sen(Pi - a).cos(Pi - a) + sen(Pi - a)] '](/latexrender/pictures/12b943f403b054b66b44ce694e29cb62.png)
. Dentro dessa derivada tem outro produto, dai fico sem saber como proceder, como aplicar a regra da cadeia corretamente.
-
Nandodtx
- Novo Usuário

-
- Mensagens: 6
- Registrado em: Sáb Mai 28, 2011 23:51
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Eng. Automação e Controle de processos
- Andamento: cursando
 por LuizAquino » Dom Mai 29, 2011 11:15
por LuizAquino » Dom Mai 29, 2011 11:15
Confira a sua função. Não haverá esse 2 multiplicando toda a expressão.
Note que a sua função está no formato:
A(x) = c[f(g(x))h(g(x)) + f(g(x))].
Isso é o mesmo que:
A(x) = c[h(g(x)) + 1]f(g(x)).
Desse modo, temos que:
A'(x) = c{[h(g(x)) + 1]'f(g(x)) + (h(g(x)) + 1)[f(g(x))]'} = c[h'(g(x))g'(x)f(g(x)) + (h(g(x)) + 1)f'(g(x))g'(x)].
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por Nandodtx » Dom Mai 29, 2011 12:26
por Nandodtx » Dom Mai 29, 2011 12:26
Cara, valeu meeesmo. Consegui aqui. Deu um pouco de trabalho mais deu certo. A derivada ficou:
![y= 2a^2 [2[cos(Pi -a)]^2 + cos(Pi - a) -1] y= 2a^2 [2[cos(Pi -a)]^2 + cos(Pi - a) -1]](/latexrender/pictures/e9f246146c71692f8a1988c14e27d2a5.png)
Dai fica facil. Resposta final a = 120º
-
Nandodtx
- Novo Usuário

-
- Mensagens: 6
- Registrado em: Sáb Mai 28, 2011 23:51
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Eng. Automação e Controle de processos
- Andamento: cursando
 por LuizAquino » Dom Mai 29, 2011 12:54
por LuizAquino » Dom Mai 29, 2011 12:54
Confira novamente a função e as suas derivadas.
A função é:
![A(\alpha) = \frac{a^2}{9}[\cos(\pi - \alpha) + 1]\textrm{sen}\, (\pi - \alpha) A(\alpha) = \frac{a^2}{9}[\cos(\pi - \alpha) + 1]\textrm{sen}\, (\pi - \alpha)](/latexrender/pictures/385eed659c85df30319fff30056e2eaf.png)
.
Desse modo, temos que:
![A^\prime(\alpha) = \frac{a^2}{9}[\textrm{sen}^2\, (\pi - \alpha) - \cos^2(\pi - \alpha) - \cos(\pi - \alpha)] A^\prime(\alpha) = \frac{a^2}{9}[\textrm{sen}^2\, (\pi - \alpha) - \cos^2(\pi - \alpha) - \cos(\pi - \alpha)]](/latexrender/pictures/05d6154f17c3b98fc1a3f37fea5023df.png)
.
Mas, isso é o mesmo que:
![A^\prime(\alpha) = \frac{a^2}{9}[1-2\cos^2(\pi - \alpha) - \cos(\pi - \alpha)] A^\prime(\alpha) = \frac{a^2}{9}[1-2\cos^2(\pi - \alpha) - \cos(\pi - \alpha)]](/latexrender/pictures/aba8a17653fa1eb649ba7ae7ee573767.png)
.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por Nandodtx » Dom Mai 29, 2011 14:37
por Nandodtx » Dom Mai 29, 2011 14:37
Realmente, procurei e achei meu erro. Contudo os pontos em que a derivada foi zero são -1 e 1/2 e fazendo o estudo do sinal da função achei que o ponto de max fica no ponto (1/2, F(1/2)). Ajudou muuuiito. Deu pra tirar varias duvidas numa questão só. To começando a vida de universitário agora, to vendo que vo usar mto esse forum aqui.
Show a atenção de vcs com nossas duvidas. Abrçs!
-
Nandodtx
- Novo Usuário

-
- Mensagens: 6
- Registrado em: Sáb Mai 28, 2011 23:51
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Eng. Automação e Controle de processos
- Andamento: cursando
 por LuizAquino » Dom Mai 29, 2011 20:55
por LuizAquino » Dom Mai 29, 2011 20:55
Na verdade, as raízes da equação

são
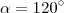
e
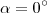
.
O ponto de máximo é (120°,
A(120°)).
SugestãoEu acredito que os tópicos abaixo podem lhe interessar:
Aulas de Matemática no YouTubeviewtopic.php?f=120&t=3818Curso de Cálculo I no YouTubeviewtopic.php?f=137&t=4280
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por Nandodtx » Seg Mai 30, 2011 10:22
por Nandodtx » Seg Mai 30, 2011 10:22
é, so que eu fiz cos(Pi-a) = x .Dai o ponto de max vai ser quando x = 1/2 ou x = -1, ou seja, quando alfa for 120º ou 0º
-
Nandodtx
- Novo Usuário

-
- Mensagens: 6
- Registrado em: Sáb Mai 28, 2011 23:51
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Eng. Automação e Controle de processos
- Andamento: cursando
 por LuizAquino » Seg Mai 30, 2011 11:44
por LuizAquino » Seg Mai 30, 2011 11:44
Vale lembrar que a variável independente original da função é alfa e não x. Por esse motivo que o correto é você dizer que o ponto de máximo ocorre quando alfa = 120°. Note que o fato de você ter feito a substituição "cos(pi - alfa) = x" foi apenas para poder resolver a equação

.
Além disso, ao contrário do que você disse, quando alfa = 0° irá ocorrer um ponto de mínimo e não de máximo.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Aplicacoes de derivadas
 por aline_n » Qui Jun 02, 2011 17:29
por aline_n » Qui Jun 02, 2011 17:29
- 1 Respostas
- 3765 Exibições
- Última mensagem por LuizAquino

Qui Jun 02, 2011 20:34
Cálculo: Limites, Derivadas e Integrais
-
- [Derivadas - Aplicações]
por Scheu » Sex Mar 16, 2012 00:01
- 1 Respostas
- 1838 Exibições
- Última mensagem por MarceloFantini

Sex Mar 16, 2012 03:17
Cálculo: Limites, Derivadas e Integrais
-
- Aplicações de Derivadas
 por lucasabreuo » Seg Mai 06, 2019 11:56
por lucasabreuo » Seg Mai 06, 2019 11:56
- 2 Respostas
- 5553 Exibições
- Última mensagem por adauto martins

Dom Jul 07, 2019 17:07
Cálculo: Limites, Derivadas e Integrais
-
- derivadas e suas aplicações
por ssousa3 » Sex Mai 27, 2011 18:07
- 11 Respostas
- 8695 Exibições
- Última mensagem por ssousa3

Sáb Mai 28, 2011 22:13
Cálculo: Limites, Derivadas e Integrais
-
- [Aplicações Derivadas] Dúvida exerc 1
por MrJuniorFerr » Sáb Out 20, 2012 01:21
- 3 Respostas
- 2622 Exibições
- Última mensagem por Russman

Sáb Out 20, 2012 02:43
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 4 visitantes
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.






![y = 2a^2 [sen(Pi - a).cos(Pi - a) + sen(Pi - a)] /9 y = 2a^2 [sen(Pi - a).cos(Pi - a) + sen(Pi - a)] /9](/latexrender/pictures/9a3980c85bb3ac53b51b6f2a657f22c9.png)
![[sen(Pi - a).cos(Pi - a) + sen(Pi - a)] ' [sen(Pi - a).cos(Pi - a) + sen(Pi - a)] '](/latexrender/pictures/12b943f403b054b66b44ce694e29cb62.png) . Dentro dessa derivada tem outro produto, dai fico sem saber como proceder, como aplicar a regra da cadeia corretamente.
. Dentro dessa derivada tem outro produto, dai fico sem saber como proceder, como aplicar a regra da cadeia corretamente.

![y= 2a^2 [2[cos(Pi -a)]^2 + cos(Pi - a) -1] y= 2a^2 [2[cos(Pi -a)]^2 + cos(Pi - a) -1]](/latexrender/pictures/e9f246146c71692f8a1988c14e27d2a5.png)

![A(\alpha) = \frac{a^2}{9}[\cos(\pi - \alpha) + 1]\textrm{sen}\, (\pi - \alpha) A(\alpha) = \frac{a^2}{9}[\cos(\pi - \alpha) + 1]\textrm{sen}\, (\pi - \alpha)](/latexrender/pictures/385eed659c85df30319fff30056e2eaf.png) .
.![A^\prime(\alpha) = \frac{a^2}{9}[\textrm{sen}^2\, (\pi - \alpha) - \cos^2(\pi - \alpha) - \cos(\pi - \alpha)] A^\prime(\alpha) = \frac{a^2}{9}[\textrm{sen}^2\, (\pi - \alpha) - \cos^2(\pi - \alpha) - \cos(\pi - \alpha)]](/latexrender/pictures/05d6154f17c3b98fc1a3f37fea5023df.png) .
.![A^\prime(\alpha) = \frac{a^2}{9}[1-2\cos^2(\pi - \alpha) - \cos(\pi - \alpha)] A^\prime(\alpha) = \frac{a^2}{9}[1-2\cos^2(\pi - \alpha) - \cos(\pi - \alpha)]](/latexrender/pictures/aba8a17653fa1eb649ba7ae7ee573767.png) .
.

 são
são 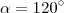 e
e 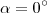 .
.

 .
.
 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , mas negativo pois tem de ser no quarto quadrante. Se
, mas negativo pois tem de ser no quarto quadrante. Se  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.