O problema parece ser simples, mas já tentei resolver várias vezes e não consegui. Segue o mesmo abaixo:
"A função z = f (x,y) tem no ponto (1,2) derivada direcional igual a
![\sqrt[2]{2} \sqrt[2]{2}](/latexrender/pictures/a8f8ae3924f6c44624745ca9e588cae3.png) , na direção do vetor v = (2,2), e derivada direcional igual a -1 na direção do vetor u = (0,1). Nessas condições pode-se afirmar:
, na direção do vetor v = (2,2), e derivada direcional igual a -1 na direção do vetor u = (0,1). Nessas condições pode-se afirmar:a) O vetor gradiente, no ponto (1,2), é igual a (3,-1). Verdadeiro ou falso?
b) Na direção do vetor (2,6) não há variação da função. Verdadeiro ou falso?"
Estou com dificuldade para resolver esse problema porque não foi dada a função f(x,y).


 é dada por:
é dada por: 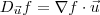 .
. .
.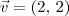 temos que
temos que  .
. temos que
temos que  .
. . Isto é, basta verificar se é válido que
. Isto é, basta verificar se é válido que 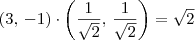 .
.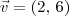 é verdade que
é verdade que  . Para isso, aqui vai uma dica: da segunda informação do exercício, temos que
. Para isso, aqui vai uma dica: da segunda informação do exercício, temos que  .
.
 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.
