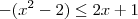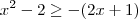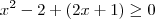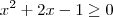Primeiro, vale lembrar que temos a
inequação modular 
e não uma "equação modular".
Como lembrou o colega Molina, nós teremos dois casos:
(i)
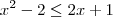
, se
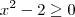
;
(ii)
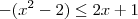
, se
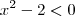
.
Note que isso é equivalente a:
(i)
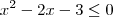
, se
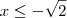
ou
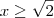
;
(ii)
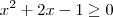
, se
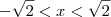
.
Resolvendo (i), temos que
![S_1 = \{(-\infty,\, -\sqrt{2}] \cup [\sqrt{2},\, +\infty)\}\cap [-1,\,3] = [\sqrt{2},\, 3] S_1 = \{(-\infty,\, -\sqrt{2}] \cup [\sqrt{2},\, +\infty)\}\cap [-1,\,3] = [\sqrt{2},\, 3]](/latexrender/pictures/3d510cc2656adf7fa8a5fb34020faffb.png)
.
Já resolvendo (ii), temos que
![S_2 = (-\sqrt{2},\,\sqrt{2}) \cap \{(-\infty,\,-\sqrt{2} - 1] \cup [\sqrt{2} - 1,\, +\infty)\}= [\sqrt{2} - 1,\, \sqrt{2}) S_2 = (-\sqrt{2},\,\sqrt{2}) \cap \{(-\infty,\,-\sqrt{2} - 1] \cup [\sqrt{2} - 1,\, +\infty)\}= [\sqrt{2} - 1,\, \sqrt{2})](/latexrender/pictures/9f5daaeccdfafa694dacbef10f7fbd43.png)
.
Desse modo, a solução será
![S = S_1 \cup S_2 = [\sqrt{2} - 1,\, 3] S = S_1 \cup S_2 = [\sqrt{2} - 1,\, 3]](/latexrender/pictures/6b31a093212ffd23ad80b33706a2cfae.png)
Vale a pena visualizar a interpretação geométrica dessa inequação, que é ilustrada na figura abaixo.
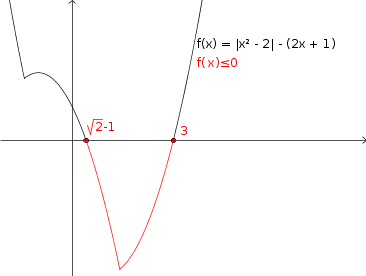
- interpretacao-geometrica.png (6.53 KiB) Exibido 1931 vezes
ObservaçãoVale destacar o desenvolvimento abaixo:
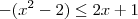
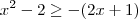
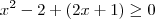
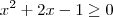 Sugestão
SugestãoBaianinha, eu gostaria de sugerir que você assista as vídeo-aulas do Nerckie sobre inequações modulares. O endereço do canal é:
http://www.youtube.com/nerckieSe suas dúvidas persistirem, então poste-as aqui.
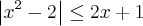 ????
????

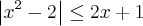 ????
????
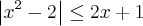
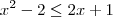
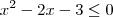
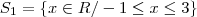
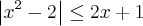
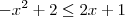

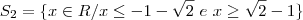
 obtemos:
obtemos: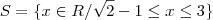


 e não uma "equação modular".
e não uma "equação modular".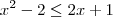 , se
, se 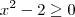 ;
;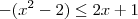 , se
, se 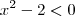 .
.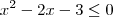 , se
, se 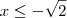 ou
ou 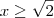 ;
;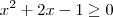 , se
, se 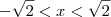 .
.![S_1 = \{(-\infty,\, -\sqrt{2}] \cup [\sqrt{2},\, +\infty)\}\cap [-1,\,3] = [\sqrt{2},\, 3] S_1 = \{(-\infty,\, -\sqrt{2}] \cup [\sqrt{2},\, +\infty)\}\cap [-1,\,3] = [\sqrt{2},\, 3]](/latexrender/pictures/3d510cc2656adf7fa8a5fb34020faffb.png) .
.![S_2 = (-\sqrt{2},\,\sqrt{2}) \cap \{(-\infty,\,-\sqrt{2} - 1] \cup [\sqrt{2} - 1,\, +\infty)\}= [\sqrt{2} - 1,\, \sqrt{2}) S_2 = (-\sqrt{2},\,\sqrt{2}) \cap \{(-\infty,\,-\sqrt{2} - 1] \cup [\sqrt{2} - 1,\, +\infty)\}= [\sqrt{2} - 1,\, \sqrt{2})](/latexrender/pictures/9f5daaeccdfafa694dacbef10f7fbd43.png) .
.![S = S_1 \cup S_2 = [\sqrt{2} - 1,\, 3] S = S_1 \cup S_2 = [\sqrt{2} - 1,\, 3]](/latexrender/pictures/6b31a093212ffd23ad80b33706a2cfae.png)