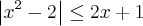 ????
????

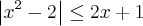 ????
????
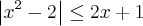
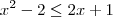
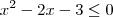
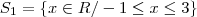
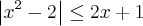
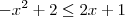

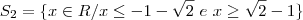
 obtemos:
obtemos: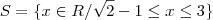


 e não uma "equação modular".
e não uma "equação modular".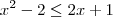 , se
, se 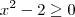 ;
;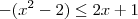 , se
, se 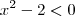 .
.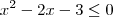 , se
, se 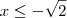 ou
ou 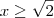 ;
;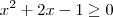 , se
, se 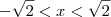 .
.![S_1 = \{(-\infty,\, -\sqrt{2}] \cup [\sqrt{2},\, +\infty)\}\cap [-1,\,3] = [\sqrt{2},\, 3] S_1 = \{(-\infty,\, -\sqrt{2}] \cup [\sqrt{2},\, +\infty)\}\cap [-1,\,3] = [\sqrt{2},\, 3]](/latexrender/pictures/3d510cc2656adf7fa8a5fb34020faffb.png) .
.![S_2 = (-\sqrt{2},\,\sqrt{2}) \cap \{(-\infty,\,-\sqrt{2} - 1] \cup [\sqrt{2} - 1,\, +\infty)\}= [\sqrt{2} - 1,\, \sqrt{2}) S_2 = (-\sqrt{2},\,\sqrt{2}) \cap \{(-\infty,\,-\sqrt{2} - 1] \cup [\sqrt{2} - 1,\, +\infty)\}= [\sqrt{2} - 1,\, \sqrt{2})](/latexrender/pictures/9f5daaeccdfafa694dacbef10f7fbd43.png) .
.![S = S_1 \cup S_2 = [\sqrt{2} - 1,\, 3] S = S_1 \cup S_2 = [\sqrt{2} - 1,\, 3]](/latexrender/pictures/6b31a093212ffd23ad80b33706a2cfae.png)
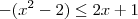
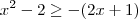
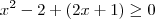
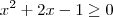

Voltar para Sistemas de Equações
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.my2009 escreveu:Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :

