Valor mínimo

por **FilipeCaceres** » Qui Mai 26, 2011 19:53

Achar o valor mínimo de $\frac{x^4+x^2+5}{(x+1)^2}$

A-1
B- 0,95
C-0,85
D- 0,75
E- 0,65

Gabarito diz que é a letra B.

Alguém tem alguma dica.

Abraço.

por **MarceloFantini** » Qui Mai 26, 2011 20:27

Minha primeira sugestão seria derivar e igualar a zero, mas não sei se "poderia" fazer isso. Já tem essas ferramentas?

por **FilipeCaceres** » Qui Mai 26, 2011 20:31

Se nós derivar isso, vamos ficar com um caminhão do 4 grau.

Teria uma outra sugestão?

por **FilipeCaceres** » Qui Mai 26, 2011 20:31

Se nós derivar isso, vamos ficar com um "caminhão" do 4 grau.

Teria uma outra sugestão?

Saiu duplicado.

por **LuizAquino** » Qui Mai 26, 2011 22:23

Abaixo há duas ilustrações do gráfico da função $f(x) = \frac{x^4+x^2+5}{(x+1)^2}$ .

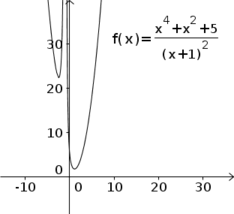
: gráfico.png (16.61 KiB) Exibido 7902 vezes

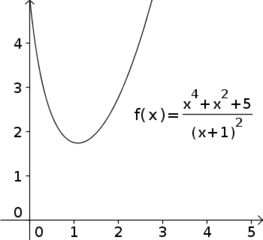
: gráfico-zoom.png (17.7 KiB) Exibido 7902 vezes

Note que o mínimo dessa função é algo no intervalo [1,5; 2].

Para essa função em particular, determinar analiticamente o valor de seu mínimo através de suas derivadas é algo bastante trabalhoso. Nesse caso, um método numérico é mais conveniente.

por **FilipeCaceres** » Qui Mai 26, 2011 22:37

Eu não posso afirmar, mas me disseram que está questão estava em um livro de questões de vestibulares militares.

Como é que eu iria resolver isso numa prova? Olhando para o gráfico eu não consigo eliminar nada.

Eu até usei o Wolfram para ver qual seria o gráfico, mas algebricamente ainda não consegui desenvolver.

por **FilipeCaceres** » Qui Mai 26, 2011 23:00

Certamente o gabarito deve estar errado.

Observem comigo e se eu estiver errado apontem meu erro.

Para que a função seja a mínima, o denoninador deve ser o máximo, logo devemos ter o maior valor de x(no intervalo 0 até 1), logo temos como resposta a Letra A.

Alguém discorda?

por **LuizAquino** » Qui Mai 26, 2011 23:21

Como eu falei, analiticamente seria muito trabalhoso! Eu acredito ser improvável que esse exercício estivesse em um vestibular. E mesmo que estivesse, há uma boa possibilidade dele ter sido anulado.

Para determinar o mínimo dessa função, vamos precisar calcular a sua derivada.

Temos que $f^\prime(x) = \frac{2(x^{4} + 2x^{3} + x - 5)}{(x + 1)^{3}}$ .

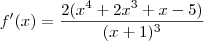
Para resolver a equação f'(x) = 0, teremos que determinar as raízes de uma equação polinomial de quarto grau dada por: $x^{4} + 2x^{3} + x - 5 = 0$ .

Note que essa equação não tem solução racional, o que já dificulta a sua solução.

Para resolvê-la analiticamente, você precisa aplicar o Método de Ferrari. Leia mais a respeito, por exemplo, no endereço:
Equação do quarto grau -- http://pt.wikipedia.org/wiki/Equa%C3%A7 ... uarto_grau

Para que a função seja a mínima o denominador deve ser o máximo, logo devemos ter o maior valor de x que nas alternativas corresponde a letra A.

Você não está levando em consideração que o numerador também está variando. Você não pode aplicar esse raciocínio nesse caso. Além disso, não confunda o valor mínimo de uma função com o valor em seu domínio que é associado a ele. Por exemplo, a função f(x) = x² - 1 tem valor mínimo igual a -1, que está associado a x = 0.

por **FilipeCaceres** » Qui Mai 26, 2011 23:31

Acabei editando antes de ver que você havia respondido, editei pois ficou muito vago, na verdade eu queria dizer que x so pode variar de 0 ate 1, pois como temos um numerador do quarto grau, qualquer valor acima de 1 ou abaixo de zero ele "crescerá" mais rápido, enquando que no intervalo de 0 até 1 ele decrescerá.

por **FilipeCaceres** » Qui Mai 26, 2011 23:38

Estava me esquecendo podemos ter os negativos também, logo podemos ter (-1,1].

Acho que agora está mais completo. :-D

por **LuizAquino** » Qui Mai 26, 2011 23:43

O seu raciocínio não está adequado.

Tanto é assim que, utilizando métodos numéricos, determinamos que o mínimo dessa função é aproximadamente 1,7397, sendo que ele ocorre para x igual a aproximadamente 1,0831.

por **FilipeCaceres** » Qui Mai 26, 2011 23:45

Eu estava relendo com calma

Além disso, não confunda o valor mínimo de uma função com o valor em seu domínio que é associado a ele.

E percebi que estava confundindo, e deu exatamente isso usando o wolfram.

por **FilipeCaceres** » Qui Mai 26, 2011 23:47

Então não tem resposta.

por **demolot** » Sex Mai 27, 2011 19:31

se for de escolha multiplica podes sempre usar a calculadora gráfica, ela consegue calcular o mínimo.
Analiticamente, 1º pensei na derivada mas ia ser muito trabalhoso fazer uma equação de 4º grau, depois se igualarmos a 0 e o denominador diferente de 0 continuamos com uma de 4º grau nao vejo outra solução se nao a calculadora