Como eu falei, analiticamente seria muito trabalhoso! Eu acredito ser improvável que esse exercício estivesse em um vestibular. E mesmo que estivesse, há uma boa possibilidade dele ter sido anulado.
Para determinar o mínimo dessa função, vamos precisar calcular a sua derivada.
Temos que
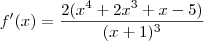
.
Para resolver a equação f'(x) = 0, teremos que determinar as raízes de uma equação polinomial de quarto grau dada por:

.
Note que essa equação não tem solução racional, o que já dificulta a sua solução.
Para resolvê-la analiticamente, você precisa aplicar o Método de Ferrari. Leia mais a respeito, por exemplo, no endereço:
Equação do quarto grau --
http://pt.wikipedia.org/wiki/Equa%C3%A7 ... uarto_grauPara que a função seja a mínima o denominador deve ser o máximo, logo devemos ter o maior valor de x que nas alternativas corresponde a letra A.
Você não está levando em consideração que o numerador também está variando. Você não pode aplicar esse raciocínio nesse caso. Além disso, não confunda o valor mínimo de uma função com o valor em seu domínio que é associado a ele. Por exemplo, a função f(x) = x² - 1 tem valor mínimo igual a -1, que está associado a x = 0.








 .
.


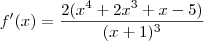 .
. .
.









 , avisa que eu resolvo.
, avisa que eu resolvo.

