





norberto escreveu:Oi Marcelo !
Talvez estejamos os dois com "conceitos errados".
Pois a resposta para sua pergunta "Você consegue contar todos os números Naturais ?" é :
- sim, claro que eu posso.
Não foi justamente isso que Cantor fez ?
Minha dúvida permanece.
Se os números Naturais são todos finitos, como podemos dizer que eles formam um
conjunto infinito ?
Eu nunca havia me perguntado isso antes, até ler um artigo em http://naturaisetransfinitos.blogspot.com
mais especificamente : http://naturaisetransfinitos.blogspot.c ... de-ou.html
Não concordo com tudo que o cara fala, mas sobre essa questão específica, o artigo fundiu minha cuca.








 finito, o conjunto
finito, o conjunto 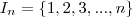 é finito. Isto é bom e serve para definir o que é um conjunto finito: dizemos que um conjunto X é finito quando é vazio ou então existem
é finito. Isto é bom e serve para definir o que é um conjunto finito: dizemos que um conjunto X é finito quando é vazio ou então existem  e uma bijeção
e uma bijeção  . Escrevendo
. Escrevendo 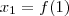 ,
, 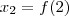 , ...,
, ..., 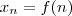 temos então
temos então  . A bijeção f chama-se uma contagem dos elementos de X e o número n chama-se o número de elementos, ou número cardinal do conjunto finito X.
. A bijeção f chama-se uma contagem dos elementos de X e o número n chama-se o número de elementos, ou número cardinal do conjunto finito X.  é finito se, e somente se, é limitado. Usando disso, é fácil de perceber que o conjunto dos naturais é infinito, pois não existe
é finito se, e somente se, é limitado. Usando disso, é fácil de perceber que o conjunto dos naturais é infinito, pois não existe  tal que exista uma bijeção
tal que exista uma bijeção 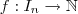 , ou seja, o conjunto dos números naturais não é limitado.
, ou seja, o conjunto dos números naturais não é limitado.

 de
de 
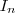 com n elementos
com n elementos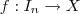
 é finito.
é finito. de
de 
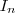 com n elementos
com n elementos é finito
é finito
 , com o número finito m de elementos,
, com o número finito m de elementos, 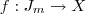 exista.
exista.  ser determinável ou não, são outros quinhentos.
ser determinável ou não, são outros quinhentos. bolinhas de gude, cada uma com o volume de
bolinhas de gude, cada uma com o volume de 
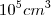
 bolinhas de gude, cada uma com o volume de
bolinhas de gude, cada uma com o volume de 
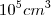
 bolinhas
bolinhas é infinito, mas todas dão voltas sobre o mesmo ponto.
é infinito, mas todas dão voltas sobre o mesmo ponto. o conjunto formado por todos os números que pudermos escrever, dadas as limitações acima
o conjunto formado por todos os números que pudermos escrever, dadas as limitações acima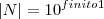
 = { 0, 1, 2, 3, ... , 99 }
= { 0, 1, 2, 3, ... , 99 }
 é
é 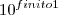
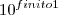 é um número finito, isso implica que a cardinalidade de
é um número finito, isso implica que a cardinalidade de  , também é finita.
, também é finita.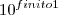 , usa finito1 para dizer a quantidade de dígitos que podemos
, usa finito1 para dizer a quantidade de dígitos que podemos 
norberto escreveu:Oi (de novo) Jorge :
Pelo que pude perceber, você ainda deve estar no início do curso de Bacharelado
e ainda não tocaram nestas questões específicas. Você já ouviu falar num cara
chamado Georg Cantor ? Ele considerou que o conjunto dos Naturais era contável e
também o eram os Inteiros e os Racionais. Até aí tudo bem.
Meu problema não passa pela enuberabilidade dos Naturais.
Quando você estudar o Peano, vai ver que os Naturais são "endereçados" por uma
função chamada "sucessor". O sucessor de um número Natural n é n+1.
Por exemplo, o sucessor(0) é 0+1, ou seja 1. Já o sucessor(1) é 1+1, ou seja, 2.
Podemos pensar que, começando de 0, achar sucessores sucessivos é o mesmo
que "contar" quantas vezes fizemos "n+1".
Eu vivia bastante feliz com essa explicação. Mas aí, o artigo do cara me fez um alerta.
Todo Natural possui "necessariamente" um número finito de dígitos. Suponha também
que tenhamos 10 símbolos à disposição (de 0 a 9). Não consigo entender como um número
com estas características :
(a) Possua um número finito de dígitos ;
(b) Cada dígito seja representado por um símbolo ;
(c) Os símbolos são tirados de um conjunto finito (de 0 a 9).
Possa ser infinito.
Por exemplo, se eu te perguntasse quantos números você pode formar
com estes 10 símbolos "contanto que os números que você formar possuam
uma quantidade finita de dígitos", você certamente não poderia me responder.
Mas certamente você só poderia formar um número finito de "números". visto que :
Eu não concordo totalmente com o cara lá do artigo. Ele chega a afirmar que
os Reais são contáveis também. Estou estudando sua "prova".
Quanto ao fato de isso ser filosofia, e não matemática, concordo em certos aspectos.
O que o Georg Cantor fez, por exemplo, foi matemática e não filosofia. Acho que isso
é matemática, mas é "fundamento da matemática", e não "aplicação prática" da matemática.
Alguém aí poderia esclarecer esta dúvida ?
Abraços

Dado um subconjunto de
Dado o conjunto finito com n elementos
Se houver uma bijeção
Então é finito.
Mas o contrário não é verdadeiro
Dado um subconjunto de
Dado o conjunto finito com n elementos
Se é finito
Não implica que haja uma bijeção
Mas implica que deva existir um outro conjunto finito , com o número finito m de elementos,
tal que a bijeção exista.
(B2) Sim. Ela é de "INDETERMINADO" bolinhas
Dizem que os Naturais possuem um número finito de dígitos, mas não dizem que número finito é esse.
Isso nos impede de fazer a bijeção, mas não significa que sua cardinalidade é infinita.
Agora me diga, se com um número finito1 de dígitos, podemos formar uma quantidade infinita de números.
Tava pesquisando sobre o cara que escreveu o artigo. Ele diz que é um matemático amador
mas não diz se é formado em alguma coisa. Queira ou não queira, ele faz afirmações muito
intrigantes.


Mas o contrário não é verdadeiro
Dado um subconjunto de
Dado o conjunto finito com n elementos
Se é finito
Não implica que haja uma bijeção
Sim, no entanto isso não serve de nada na discussão.
(B2) Sim. Ela é de "INDETERMINADO" bolinhas
Indeterminado para você é finito?
Por favor, suponha agora num assunto não relacionado um sistema possível e indeterminado. Explicite todas as soluções já que são finitas pois é indeterminado.
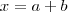
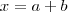
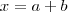
Dizem que os Naturais possuem um número finito de dígitos...
Os naturais não possuem um número finito de dígitos. ... Os naturais são um CONJUNTO.
Bom, já não confio na lógica do cara, sabendo que ele é um "matemático" amador pior ainda.
Ele não pode provar as afirmações dele,

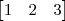 , tendo portanto 3 casas.
, tendo portanto 3 casas.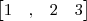 , tendo portanto 4 casas.
, tendo portanto 4 casas.

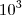 como ordem de grandeza.
como ordem de grandeza.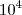
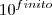 .
.
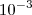
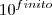 , a segunda
, a segunda 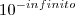
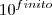 dos possíveis números na primeira matriz descreve a quantidade de casas do segundo exemplo (Antes que o fantini venha dizer que meu finito está variando, quero adiantar que não. Ele só não foi informado.) , justamente pelo fato de que
dos possíveis números na primeira matriz descreve a quantidade de casas do segundo exemplo (Antes que o fantini venha dizer que meu finito está variando, quero adiantar que não. Ele só não foi informado.) , justamente pelo fato de que 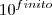 nunca vai
nunca vai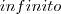 número de "casas" da segunda matriz, não importando o quão grande este finito seja.
número de "casas" da segunda matriz, não importando o quão grande este finito seja.
norberto escreveu:(...)
(1) Pense no maior número que você puder :
Pensei.
Ops! quer dizer, sei que ele não é o maior.
Desisto. Não consigo pensar em um que seja o maior.
Mas não se preocupe. Entendi o "espírito".
(...)

norberto escreveu:(...)
A medida que eu "aumento" a quantidade de colunas do primeiro exemplo, eu aumento a ordem de grandeza dos números que podem ser representados por esta matriz.
[ 1 2 3 ], por exemplo temcomo ordem de grandeza.
[1 2 3 9] tem
Pela própria definição da matriz, só posso pensar em números de grandeza.
(...)

Pela própria definição da matriz, só posso pensar em números de grandeza.
Por que? Note que você pode adicionar quantas casas precisar para representar o número.
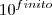 .
.... não há um número máximo fixo k de casas.

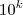 produz um número finito, mas indeterminado, ou indeterminável.
produz um número finito, mas indeterminado, ou indeterminável.Vamos imaginar por um momento que haja esse número máximo k de casas.
Deste modo, o número [9 9 9 9 ... 9 9 9 9 ] (com k casas) seria o maior natural possível.
 a
a  ser infinito por natureza,
ser infinito por natureza,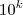 elementos.
elementos.Ops! Isso é uma contradição! Como você mesmo havia percebido antes, não pode haver o maior natural!
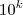 elementos.
elementos.Além disso, note que podemos obter outra contradição quando partimos dessa suposição de termos no máximo k casas. O número natural acima tem o sucessor com k+1 casas: [1 0 0 0 ... 0].
Vamos imaginar por um momento que haja esse número máximo k de casas.
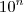 ? E de
? E de 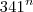 ?
?

noberto escreveu:Eu concordo. Nunca duvidei disso e talvez, essa certeza é que esteja me fazendo ver essa questão como um grande paradoxo.
Eu penso que :
Não há um número máximo fixo k de casas. Por outro lado, existe uma limitação. A de que o número de casas é finito.
noberto escreveu:(q) Considere o número natural finito n. O que podemos afirmar de? E de
?
Algumas respostas válidas seriam.
r1. O primeiro é par e o segundo é ímpar.
r2. O segundo é um número finito maior que o primeiro.
noberto escreveu:Além disso, note que podemos obter outra contradição quando partimos dessa suposição de termos no máximo k casas. O número natural acima tem o sucessor com k+1 casas: [1 0 0 0 ... 0].
Ops ! Você se esqueceu de como você definiu k.Vamos imaginar por um momento que haja esse número máximo k de casas.

Na minha opinião, você está andando em círculos!
Eu concordo. Nunca duvidei disso e talvez, essa certeza é que esteja me fazendo ver essa questão como um grande paradoxo.
Não há um número máximo fixo k de casas. Por outro lado, existe uma limitação. A de que o número de casas é finito.
Não há paradoxo nessa afirmação. Isso porque, apesar de cada número ter uma quantidade de casas finita, essa quantidade pode variar (ilimitadamente) de um número para o outro (isto é, não há uma quantidade máxima de casas).
Apenas quando você convencer-se disso é que irá parar de correr em círculos. Infelizmente, por mais que eu queira ajudar, isso é algo que só você pode fazer.
(q) Considere o número natural finito n. O que podemos afirmar de? E de
?
Algumas respostas válidas seriam.
r1. O primeiro é par e o segundo é ímpar.
r2. O segundo é um número finito maior que o primeiro.
Considerando que "natural finito" ou "número finito" quer dizer que o número tem finitas casas, ambas as respostas estão corretas.
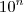 é finito
é finito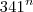 é finito
é finito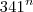 é maior que
é maior que 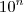
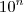 pode ser traduzido por :
pode ser traduzido por :
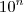 ?
?

Sob sua opinião que :Apenas quando você convencer-se disso é que irá parar de correr em círculos. Infelizmente, por mais que eu queira ajudar, isso é algo que só você pode fazer.
Isto tornaria a matemática uma questão de fé. Deus existe ? E matinta-pereira ?
Não. Isso não é algo que dependa exatamente de mim.
Sempre achei teus argumentos uma excelência. Mas realmente, peço desculpas por não ter entendido o exemplo do "k+1". Sinceramente, achei que a afirmação não cabia, pois partimos já da presunção que k era máximo. Se quiséssemos provar que k não poderia ser máximo, baseado na afirmativa de que "todo número natural tem um sucessor", não precisaríamos da matriz. O argumento seria simples :
. Suponha que K seja um número máximo ;
. Considere que K+1 é o sucessor de K.
Como as duas afirmações levam a uma contradição, qualquer uma delas poderia ser falsa se considerássemos a outra verdadeira.
Mas como eu disse, isso pode ser um erro de interpretação MEU.
I. Não podemos dizer que exista um número k máximo de "casas", na formação de um número natural.
II. O número de "casas", porém é finito.
III. Isto não é um paradoxo.
Logo, o que considero como PARADOXO é a conclusão disto tudo.
O conjunto dos naturais possui infinitos elementos, todos finitos.
Ora como "TODOS" os naturais possui finitas casas, não posso imaginar como isso seria possível.

LuizAquino escreveu:As três afirmações são verdadeiras.
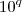 é especificamente, o número de elementos de um conjunto, cujos elementos são escritos pela combinação de
é especificamente, o número de elementos de um conjunto, cujos elementos são escritos pela combinação de 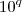 elementos, todos com uma quantidade finita de casas
elementos, todos com uma quantidade finita de casas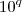 elementos, todos com uma q
elementos, todos com uma q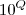 é um número finito. E ainda é par.
é um número finito. E ainda é par.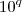 elementos é infinito, mas
elementos é infinito, mas 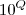 é um número finito ?
é um número finito ?LuizAquino escreveu:... apesar de todo número natural ter uma quantidade de casas limitada, essa quantidade pode variar ilimitadamente...

... apesar de todo número natural ter uma quantidade de casas limitada, essa quantidade pode variar ilimitadamente...
Pode ser que quem esteja "variando" seja eu (afinal estou andando em círculos), mas "limitado" que varia "ilimitadamente" é bem paradoxal, não é ?


S = {1, 10, 100, 1000, 10000, ...}
A quantidade de elementos deste conjunto é justamente q, se considerarmos q uma abreviação da frase "número finito de casas".
E o "número finito de casas", por ser "finito", é finito.
Logo o número de elementos de S, por ter o mesmo valor de q, também o é.
E "número finito de casas" não é a grandeza que estaria "variando".
Mas concordo que o "número específico de casas de cada elemento", seja uma grandeza "limitada" por q e que está variando.
Mas não "ilimitadamente", pois, como disse, ela é limitada por "número finito de casas".
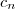 é a quantidade de casas do n-ésimo termo dessa sequência, então
é a quantidade de casas do n-ésimo termo dessa sequência, então  . Note como fica evidente que a quantidade de casas específica de cada termo é limitada, porém essa quantidade pode variar sem um limite de termo para termo. Ou seja, não existe um número q tal que
. Note como fica evidente que a quantidade de casas específica de cada termo é limitada, porém essa quantidade pode variar sem um limite de termo para termo. Ou seja, não existe um número q tal que 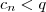 para todo termo n. A sua interpretação de que esse número existe, mas que "(...) não 'especificamos' que diacho de 'número finito é este' (...)" está equivocada.
para todo termo n. A sua interpretação de que esse número existe, mas que "(...) não 'especificamos' que diacho de 'número finito é este' (...)" está equivocada.

LuizAquino escreveu:Você está equivocado.
LuizAquino escreveu:A progressão geométrica S = {1, 10, 100, 1000, ...} possui infinitos termos e não é pelo fato que você mencionou no final de sua mensagem!
LuizAquino escreveu:Não existe um número q que limite a quantidade de casas! Você precisa definitivamente entender isso!
LuizAquino escreveu:A afirmação de que cada termo dessa sequência tem um "número finito de casas", apenas significa que não há um termo com infinitas casas. Mas, essa restrição não impede que esse número de casas possa variar sem limites de termo para termo!

norberto escreveu:Me desculpe, mas acho que desta vez é você que está andando em círculos com o conceito de algo "limitado" que varia "ilimitadamente".
 para todos os termos i e j distintos da sequência. Isso significa que a variação entre a quantidade de casas não é limitada. O que é limitada, sim, é a quantidade de casas que cada termo individualmente pode ter.
para todos os termos i e j distintos da sequência. Isso significa que a variação entre a quantidade de casas não é limitada. O que é limitada, sim, é a quantidade de casas que cada termo individualmente pode ter.
LuizAquino escreveu:Note que não há um número r que faça ser válida a desigualdadepara todos os termos i e j distintos da sequência. Isso significa que a variação entre a quantidade de casas não é limitada. O que é limitada, sim, é a quantidade de casas que cada termo individualmente pode ter.
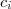 no conjunto de "número de casas" que seja o último elemento. Mas os elementos deste conjunto, não crescem "ilimitadamente". Eles crescem de acordo com a limitação de serem todos "números finitos de casas". O que não acontece com o conjunto "número de casa decimais".
no conjunto de "número de casas" que seja o último elemento. Mas os elementos deste conjunto, não crescem "ilimitadamente". Eles crescem de acordo com a limitação de serem todos "números finitos de casas". O que não acontece com o conjunto "número de casa decimais".
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , mas negativo pois tem de ser no quarto quadrante. Se
, mas negativo pois tem de ser no quarto quadrante. Se  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.