A = 6*x² e V = x*x² ou x^3
Se fosse o cont rário, seria assim:
V(A) = x*x² = (x²=A/6) ---> (A/6)*(?A/6) ---> f(x) = (x/6)*(?x/6), mas se eu fizer o q o enunc iado pede, ao mesmo modo da resolução anterior, não consigo:
Ex:
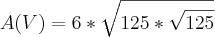
Não estou conseguindo o resultado satisfatório, alguém tem alguma dica para resolver isso?
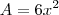, ![V=x^3 = x \cdot x^2 = \sqrt{\frac{A}{6}} \cdot \frac{A}{6} \Rightarrow A = \sqrt[3]{6 \sqrt{6}V}](/latexrender/pictures/732927c7d66cda95fc2558031bce67eb.png "V=x^3 = x \cdot x^2 = \sqrt{\frac{A}{6}} \cdot \frac{A}{6} \Rightarrow A = \sqrt[3]{6 \sqrt{6}V}")
![A=6x^2, V=x^3 = x \cdot x^2 = \sqrt{\frac{A}{6}} \cdot \frac{A}{6} \Rightarrow A = \sqrt[3]{6 \sqrt{6}V}](/latexrender/pictures/65049ee8aa3ae07d85dfae90d8f66d09.png "A=6x^2, V=x^3 = x \cdot x^2 = \sqrt{\frac{A}{6}} \cdot \frac{A}{6} \Rightarrow A = \sqrt[3]{6 \sqrt{6}V}")
![V=x^3\,\therefore x=\sqrt[3]{V}](/latexrender/pictures/bfe600616dc7c28b1115b82e09c67dca.png "V=x^3\,\therefore x=\sqrt[3]{V}")
![A=6.\sqrt[3]{V^2}](/latexrender/pictures/894219b5934a1182dad1fedca96d3347.png "A=6.\sqrt[3]{V^2}")
![A=6.(\sqrt[3]{V})^2](/latexrender/pictures/fd06720af0249770400109d33edabe20.png "A=6.(\sqrt[3]{V})^2")
![f(x) = 6*{(\sqrt[3]{x})}^{2}](/latexrender/pictures/f95549f45d5fe74dc221d624014d509f.png "f(x) = 6*{(\sqrt[3]{x})}^{2}")
por