 por Diana » Seg Mai 23, 2011 22:10
por Diana » Seg Mai 23, 2011 22:10
Um polígono convexo A, possui 3 lados a mais que um poligono convexo B, quanto às diagonais, o polígono A possui 12 diagonais a mais que o polígono B. Determine quais são os polígonos A e B.
Resposta: heptágono e quadrilátero
Formula d=(n-3).n / 2
Eu faço e não chego a nada, o máximo que eu consegui foi que n de A é o n de B mais 4, e esta errado...
-
Diana
- Novo Usuário

-
- Mensagens: 9
- Registrado em: Ter Mai 03, 2011 00:03
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por FilipeCaceres » Seg Mai 23, 2011 22:27
por FilipeCaceres » Seg Mai 23, 2011 22:27
Façamos o seguinte,

=lados de A

=lados de B
Assim temos,


Logo,

Substituindo o valor de


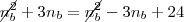

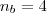
, que corresponde ao quadrado.
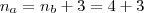

, que corresponde ao heptágono.
Abraço.
-
FilipeCaceres
- Colaborador Voluntário

-
- Mensagens: 351
- Registrado em: Dom Out 31, 2010 21:43
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Tec. Mecatrônica
- Andamento: formado
 por Diana » Seg Mai 23, 2011 22:45
por Diana » Seg Mai 23, 2011 22:45
Eu entendi, mas mais ou menos. entendi até quando você substituiu os valores, mas nao encontrei de onde saiu o 24, e por que o 2 em baixo nao ta mais la. será que teria como voce me explicar? desculpa...
-
Diana
- Novo Usuário

-
- Mensagens: 9
- Registrado em: Ter Mai 03, 2011 00:03
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por FilipeCaceres » Seg Mai 23, 2011 22:56
por FilipeCaceres » Seg Mai 23, 2011 22:56
Escrevendo errado vais er difícil de entender mesmo

Logo,

Substituindo o valor de n_a

Corrigindo.
Sabemos que:

Assim temos,

Substituindo o valor de

,
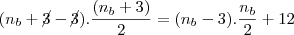
Multiplicando tudo por 2 e resolvendo temos
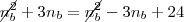
O resto é igual.
Abraço.
-
FilipeCaceres
- Colaborador Voluntário

-
- Mensagens: 351
- Registrado em: Dom Out 31, 2010 21:43
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Tec. Mecatrônica
- Andamento: formado
 por Diana » Seg Mai 23, 2011 23:19
por Diana » Seg Mai 23, 2011 23:19
Agora sim! entendi direitinho, brigadão mesmo! abraço
-
Diana
- Novo Usuário

-
- Mensagens: 9
- Registrado em: Ter Mai 03, 2011 00:03
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
Voltar para Geometria Plana
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Polígonos] questão sobre polígonos
por -daniel15asv » Qui Ago 02, 2012 20:11
- 2 Respostas
- 2168 Exibições
- Última mensagem por -daniel15asv

Sex Ago 03, 2012 00:24
Geometria Plana
-
- Poligonos
por cristina » Qui Abr 15, 2010 19:37
- 1 Respostas
- 3250 Exibições
- Última mensagem por Elcioschin

Qui Abr 15, 2010 20:25
Geometria Plana
-
- Poligonos
 por Jean Cigari » Qui Jun 30, 2011 13:50
por Jean Cigari » Qui Jun 30, 2011 13:50
- 1 Respostas
- 3805 Exibições
- Última mensagem por FilipeCaceres

Qui Jun 30, 2011 20:29
Geometria Plana
-
- poligonos com PA
por alfabeta » Qua Mar 07, 2012 20:39
- 1 Respostas
- 4238 Exibições
- Última mensagem por MarceloFantini

Qua Mar 07, 2012 23:49
Geometria Plana
-
- Polígonos não-convexos
por maria cleide » Sáb Set 24, 2011 23:03
- 1 Respostas
- 1813 Exibições
- Última mensagem por maria cleide

Qui Set 29, 2011 21:03
Geometria Plana
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
cálculo de limites
Autor:
Hansegon - Seg Ago 25, 2008 11:29
Bom dia.
Preciso de ajuda na solução deste problema, pois só chego ao resultado de 0 sobre 0.
Obrigado
\lim_{x\rightarrow-1} x³ +1/x²-1[/tex]
Assunto:
cálculo de limites
Autor:
Molina - Seg Ago 25, 2008 13:25

Realmente se você jogar o -1 na equação dá 0 sobre 0.
Indeterminações deste tipo você pode resolver por L'Hôpital
que utiliza derivada.
Outro modo é transformar o numerador e/ou denominador
para que não continue dando indeterminado.
Dica: dividir o numerador e o denominador por algum valor é uma forma que normalmente dá certo.

Caso ainda não tenha dado uma

, avisa que eu resolvo.
Bom estudo!
Assunto:
cálculo de limites
Autor:
Guill - Dom Abr 08, 2012 16:03



Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


 =lados de A
=lados de A =lados de B
=lados de B



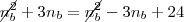

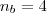 , que corresponde ao quadrado.
, que corresponde ao quadrado.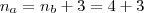
 , que corresponde ao heptágono.
, que corresponde ao heptágono.


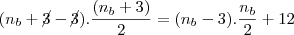


 , avisa que eu resolvo.
, avisa que eu resolvo.

