A)
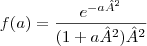
B)
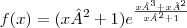
c)
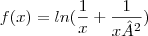
Tentei, mas só chego em resultados errados


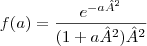
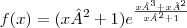
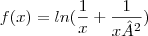


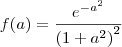
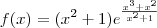
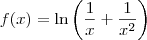
![f^\prime(a)=\frac{\left({e}^{-a^2}\right)^\prime \left(1+a^2\right)^2 - {e}^{-a^2}\left[\left(1+a^2\right)^2\right]^\prime}{\left[\left(1+a^2\right)^2\right]^2} f^\prime(a)=\frac{\left({e}^{-a^2}\right)^\prime \left(1+a^2\right)^2 - {e}^{-a^2}\left[\left(1+a^2\right)^2\right]^\prime}{\left[\left(1+a^2\right)^2\right]^2}](/latexrender/pictures/8654db3fe9635fc6f806069f4bd0c030.png)
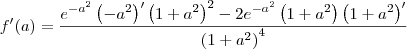
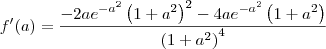
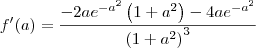
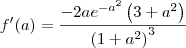

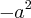 como "u" e utilizei os operadores
como "u" e utilizei os operadores 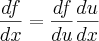 chegando ao resultado de
chegando ao resultado de 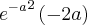
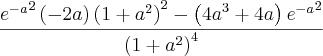


Voltar para Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 13 visitantes
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png) (dica : igualar a expressão a
(dica : igualar a expressão a  e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)