Oi Alzenir.
Antes, gostaria de te dar uma dica. Quando for postar, se possível, tenta colocar no título, mais ou menos o
assunto. Assim, se tiver um cara que "goste" do assunto no fórum, ele vai logo clicar lá.
Mas de qualquer modo, o que você precisa é gerar uma equação linear que "descreva" mais ou menos a
curva feita pelos teus dados. Como você sabe, uma equação linear tem a forma
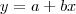
onde, no seu problema :
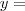
consumo

mês
Você precisa utilizar algum método para calcular o "a" e o "b" desta equação. Como o problema exige que
este método seja o dos mínimos quadrados, vamos utilizá-lo.
O método consiste em calcular 2 valores intermediários, que são :
(1)
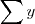
(2)
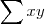
O primeiro valor é dado por :
(1)

onde K, no seu caso, representa o número de dados coletados.
Falta só você calcular
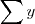
e



Você termina essa primeira etapa com a seguinte equação :
(A)

A segunda etapa é calcular :
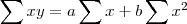
Já temos

. Só faltam os outros dois.
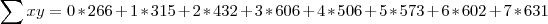
ou
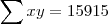
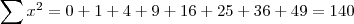
Voce termina a segunda etapa com :
(B)

Agora você pode achar
a e
b. Acho que você sabe como.
Como "dica" experimente multiplicar (A) por

e some (A) com (B).
Assim que você tiver com os valores de
a e
b, substitua-os na equação :
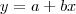
Em seguida calcule y para os meses 8, 9 e 10.
Boa sorte.


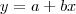
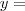 consumo
consumo mês
mês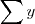
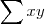
 onde K, no seu caso, representa o número de dados coletados.
onde K, no seu caso, representa o número de dados coletados.



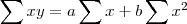
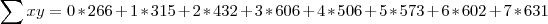
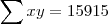
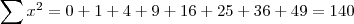

 e some (A) com (B).
e some (A) com (B).