
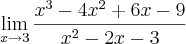
Qual seria o modo mais facil para resolvê-lo, divisao de polinomios?


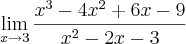


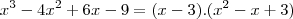
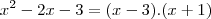





 , poderia ser dito que fiz comparação de coeficientes, mas no entanto realizei sem fazer nenhuma conta, simplesmente olhei e vi
, poderia ser dito que fiz comparação de coeficientes, mas no entanto realizei sem fazer nenhuma conta, simplesmente olhei e vi 
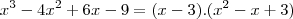


Voltar para Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 5 visitantes

 .
.



