Prova de função crescente.

por **TheoFerraz** » Seg Mai 16, 2011 20:39

Na lista de exercicios o professor pegou esse exercicio de um livro ai:

Seja $f: I \rightarrow J$ uma função bijetora. prove que ela é ou crescente, ou decrescente (monótona)

a) pelo método da análise real.

b) pelo método das derivadas.

Olha, talvez eu até consiga por derivadas, mas eu mal sei o que é bijetora! se alguém puder me ajudar seria ótimo!
Ah, e sobre essas demonstrações ai, principalmente as analíticas, existe algum livro, algum lugar que eu possa aprender essas coisas? como provar por absurdo, indução finita, essas coisas? Eu faço física mas o meu professor da a aula como se nós fizéssemos matemática pedindo para provarmos teoremas e etc, mas eu preciso saber essas coisas...

Agradeço já à qualquer ajuda! Obrigado!

por **LuizAquino** » Qua Mai 18, 2011 12:34

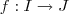Dizemos que a função $f: I \to J$ é bijetora se as duas propriedades abaixo são válidas:
(i) Para quaisquer x_1

e

pertencentes a I, se $x_1\neq x_2$ , então temos que $f(x_1)\neq f(x_2)$ ;
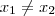(ii) Para qualquer y pertencente a J, temos que existe algum x pertencente a I tal que y = f(x).

Se uma função tem apenas a propriedade (i), então ela é chamada de injetora.

Por outro lado, se uma função tem apenas a propriedade (ii), então ela é chamada de sobrejetora.

Para resolver o quesito (a) do exercício uma boa alternativa é usar o Axioma da Tricotomia (juntamente com o fato da função ser injetora): dados dois números reais a e b apenas uma das afirmações será verdadeira:
(i) a = b
(ii) a > b
(iii) a < b

Quanto a livros com técnicas de demonstração há vários. Um deles é:
Fossa, John. Introdução às Técnicas de Demonstração na Matemática. 2ª Edição. São Paulo: Editora Livraria da Física, 2009.

Prova de função crescente.

Prova de função crescente.

Prova de função crescente.

Re: Prova de função crescente.

Quem está online