 por ewald » Ter Mai 17, 2011 15:40
por ewald » Ter Mai 17, 2011 15:40
![\lim_{x\rightarrow -\infty} \frac{\sqrt[2]{2{x}^{4}-7x+1}-{x}^{2}}{2{x}^{2}-x} \lim_{x\rightarrow -\infty} \frac{\sqrt[2]{2{x}^{4}-7x+1}-{x}^{2}}{2{x}^{2}-x}](/latexrender/pictures/6347201835d8f34ee8ccdffb2e8ead40.png)
To com dificuldade nessa. Eu to tentando fazer dividindo em cima e em baixo por x² e assim ficar com 2 no denominador (se nao tiver errado no calculo), porem o problema é na raiz. Na raiz eu devo dividir por x² ou por
![\sqrt[2]{{x}^{4}} \sqrt[2]{{x}^{4}}](/latexrender/pictures/2fd57a217b10e292d27f1ec0b26ec0fc.png)
... Se puder resolver esta questao pra mim eu agradeço!
-
ewald
- Usuário Dedicado

-
- Mensagens: 30
- Registrado em: Qui Mai 05, 2011 17:40
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Eletrica
- Andamento: cursando
 por Claudin » Ter Mai 17, 2011 18:51
por Claudin » Ter Mai 17, 2011 18:51
fiz rapidao aqui e achei

mas vo ter q sair aqui, dps eu faço com mais calma, e posto aqui.
abraço
"O que sabemos é uma gota, o que não sabemos é um oceano." - Isaac Newton
-
Claudin
- Colaborador Voluntário

-
- Mensagens: 913
- Registrado em: Qui Mai 12, 2011 17:34
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por LuizAquino » Qua Mai 18, 2011 11:35
por LuizAquino » Qua Mai 18, 2011 11:35
Dê uma olhada na propriedade de radiciação discutida no tópico:
Exercicio de Limite - Duvidaviewtopic.php?f=120&t=4759O valor correto desse limite é:
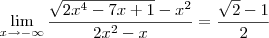
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por Claudin » Qua Mai 18, 2011 11:50
por Claudin » Qua Mai 18, 2011 11:50
Nao poderia fazer eliminando a raiz
elevando tanto o denominador quanto o numerador ao quadrado. E dps
dividir ambos pelo maior expoente?
"O que sabemos é uma gota, o que não sabemos é um oceano." - Isaac Newton
-
Claudin
- Colaborador Voluntário

-
- Mensagens: 913
- Registrado em: Qui Mai 12, 2011 17:34
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por LuizAquino » Qua Mai 18, 2011 11:55
por LuizAquino » Qua Mai 18, 2011 11:55
Claudin escreveu:Nao poderia fazer eliminando a raiz
elevando tanto o denominador quanto o numerador ao quadrado. E dps
dividir ambos pelo maior expoente?
É claro que
não!
Se você elevar o numerador e o denominador ao quadrado você altera a fração original!
Por exemplo, note que

.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por Claudin » Qua Mai 18, 2011 12:03
por Claudin » Qua Mai 18, 2011 12:03
Nao consegui chegar no resultado correto entao!
Se tiver como discriminar melhor o limite, eu agradeço!
abraço
"O que sabemos é uma gota, o que não sabemos é um oceano." - Isaac Newton
-
Claudin
- Colaborador Voluntário

-
- Mensagens: 913
- Registrado em: Qui Mai 12, 2011 17:34
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por LuizAquino » Qua Mai 18, 2011 12:40
por LuizAquino » Qua Mai 18, 2011 12:40
A estratégia para resolver esse limite já foi dita acima: dividir tanto o numerador quanto o denominador por x². Vale lembrar que será necessário usar uma propriedade de radiciação como já citei anteriormente.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por Claudin » Qua Mai 18, 2011 13:01
por Claudin » Qua Mai 18, 2011 13:01
Agora sim compreendi!
Obrigado
"O que sabemos é uma gota, o que não sabemos é um oceano." - Isaac Newton
-
Claudin
- Colaborador Voluntário

-
- Mensagens: 913
- Registrado em: Qui Mai 12, 2011 17:34
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por ewald » Qua Mai 18, 2011 14:14
por ewald » Qua Mai 18, 2011 14:14
Obrigado !!
-
ewald
- Usuário Dedicado

-
- Mensagens: 30
- Registrado em: Qui Mai 05, 2011 17:40
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Eletrica
- Andamento: cursando
 por FilipeCaceres » Qua Mai 18, 2011 14:36
por FilipeCaceres » Qua Mai 18, 2011 14:36
Seja
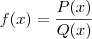
onde
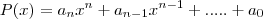
e
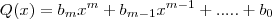
são polinômios de coeficientes reais de graus n e m, respectivamente, isto é
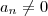
e

. Então:
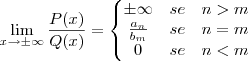
Para questão temos,

Logo,

PS:Editei para corrigir os erros de digitação.
Espero ter contribuído com algo.
Editado pela última vez por
FilipeCaceres em Qua Mai 18, 2011 15:55, em um total de 2 vezes.
-
FilipeCaceres
- Colaborador Voluntário

-
- Mensagens: 351
- Registrado em: Dom Out 31, 2010 21:43
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Tec. Mecatrônica
- Andamento: formado
 por LuizAquino » Qua Mai 18, 2011 15:10
por LuizAquino » Qua Mai 18, 2011 15:10
FilipeCaceres reveja a sua resolução:

Editado pela última vez por
LuizAquino em Qua Mai 18, 2011 15:30, em um total de 1 vez.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por FilipeCaceres » Qua Mai 18, 2011 15:18
por FilipeCaceres » Qua Mai 18, 2011 15:18
Além do erro de digitação tem algum erro conceitual?
No lugar do 1 é um x, mas em nada se altera o resultado.
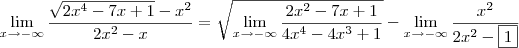
Corrigido
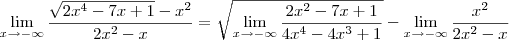
Abraço.
-
FilipeCaceres
- Colaborador Voluntário

-
- Mensagens: 351
- Registrado em: Dom Out 31, 2010 21:43
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Tec. Mecatrônica
- Andamento: formado
 por LuizAquino » Qua Mai 18, 2011 15:38
por LuizAquino » Qua Mai 18, 2011 15:38
Não há erro conceitual.
Os erros são:
1) No numerador dentro do radical deve aparecer

ao invés e

.
2) No denominador dentro do radical deve aparecer

.
3) No denominador da segunda parcela (sem o radical) deve aparecer -x ao invés de -1.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por FilipeCaceres » Qua Mai 18, 2011 15:47
por FilipeCaceres » Qua Mai 18, 2011 15:47
Nossa escrevi tudo errado.
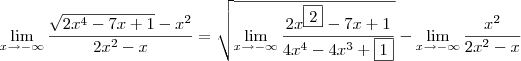
Corrigido.

Valeu.
Abraço.
-
FilipeCaceres
- Colaborador Voluntário

-
- Mensagens: 351
- Registrado em: Dom Out 31, 2010 21:43
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Tec. Mecatrônica
- Andamento: formado
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Limite indeterminado
por ewald » Qui Mai 05, 2011 17:55
- 1 Respostas
- 1847 Exibições
- Última mensagem por LuizAquino

Qui Mai 05, 2011 18:12
Cálculo: Limites, Derivadas e Integrais
-
- Limite indeterminado 0/0
por ewald » Qui Mai 05, 2011 19:08
- 1 Respostas
- 4360 Exibições
- Última mensagem por LuizAquino

Qui Mai 05, 2011 19:41
Cálculo: Limites, Derivadas e Integrais
-
- Limite indeterminado ? - ?
por cjunior94 » Ter Mai 01, 2012 22:00
- 1 Respostas
- 1870 Exibições
- Última mensagem por LuizAquino

Qua Mai 02, 2012 14:17
Cálculo: Limites, Derivadas e Integrais
-
- Duvida limite indeterminado
por ewald » Seg Mai 09, 2011 17:20
- 1 Respostas
- 2546 Exibições
- Última mensagem por LuizAquino

Seg Mai 09, 2011 20:01
Cálculo: Limites, Derivadas e Integrais
-
- Limite trigonometrico indeterminado
por ewald » Qui Mai 26, 2011 15:15
- 11 Respostas
- 5836 Exibições
- Última mensagem por MarceloFantini

Dom Mai 29, 2011 02:32
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 8 visitantes
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
zig - Sex Set 23, 2011 13:57
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
Vennom - Sex Set 23, 2011 21:41
zig escreveu:![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)
Rpz, o negócio é o seguinte:
Quando você tem uma potência negativa, tu deve inverter a base dela. Por exemplo:

Então pense o seguinte: a fração geratriz de 0,05 é

, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
Veja:
![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
A raiz quadrada de vinte, você acha fácil, né?
Espero ter ajudado.
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
fraol - Dom Dez 11, 2011 20:23
Nós podemos simplificar, um pouco,

da seguinte forma:

.
É isso.
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
fraol - Dom Dez 11, 2011 20:24
Nós podemos simplificar, um pouco,

da seguinte forma:

.
É isso.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![\lim_{x\rightarrow -\infty} \frac{\sqrt[2]{2{x}^{4}-7x+1}-{x}^{2}}{2{x}^{2}-x} \lim_{x\rightarrow -\infty} \frac{\sqrt[2]{2{x}^{4}-7x+1}-{x}^{2}}{2{x}^{2}-x}](/latexrender/pictures/6347201835d8f34ee8ccdffb2e8ead40.png)
![\sqrt[2]{{x}^{4}} \sqrt[2]{{x}^{4}}](/latexrender/pictures/2fd57a217b10e292d27f1ec0b26ec0fc.png) ... Se puder resolver esta questao pra mim eu agradeço!
... Se puder resolver esta questao pra mim eu agradeço!



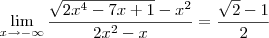

 .
.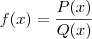
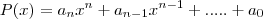 e
e 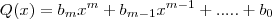 são polinômios de coeficientes reais de graus n e m, respectivamente, isto é
são polinômios de coeficientes reais de graus n e m, respectivamente, isto é 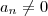 e
e  . Então:
. Então: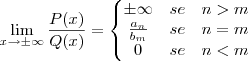


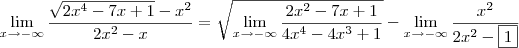
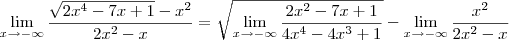
 ao invés e
ao invés e  .
. .
.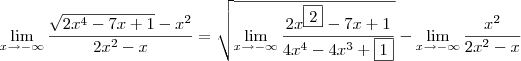
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)

 , ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio. ![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
 da seguinte forma:
da seguinte forma: .
. da seguinte forma:
da seguinte forma: .
.