Preciso de ajuda nesse problema de função: Um pequeno fabricante de vasos ornamentais vende cada um a 30,00. O custo total consiste de uma taxa fixa de 90,00 somada ao custo de produção de 12,00 por unidade.
a) quantas unidades o fabricante precisa vender para existir o nivelamento? ( nivelamento de que? )
b) o lucro ou prejuízo é a diferença entre a receita e o custo. Se foram vendidos 3 vasos, houve lucro ou prejuízo?
c) quantas unidades o fabricante deverá vender se quiser obter um lucro de 270,00?


 função Valor. Se o valor for positivo é lucro, se for negativo é prejuízo.
função Valor. Se o valor for positivo é lucro, se for negativo é prejuízo.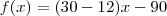
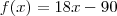
 em ordem a
em ordem a 