 por FilipeCaceres » Seg Mai 16, 2011 23:05
por FilipeCaceres » Seg Mai 16, 2011 23:05
-
FilipeCaceres
- Colaborador Voluntário

-
- Mensagens: 351
- Registrado em: Dom Out 31, 2010 21:43
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Tec. Mecatrônica
- Andamento: formado
 por Claudin » Seg Mai 16, 2011 23:19
por Claudin » Seg Mai 16, 2011 23:19
No segundo exemplo
é log na base 3 ou na base 2?
"O que sabemos é uma gota, o que não sabemos é um oceano." - Isaac Newton
-
Claudin
- Colaborador Voluntário

-
- Mensagens: 913
- Registrado em: Qui Mai 12, 2011 17:34
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por jamiel » Seg Mai 16, 2011 23:50
por jamiel » Seg Mai 16, 2011 23:50
Mas como vc transformou uma raiz em uma potência. 3^1/2 é 1,5, não?
-
jamiel
- Colaborador Voluntário

-
- Mensagens: 131
- Registrado em: Seg Jan 31, 2011 15:48
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Mecânica
- Andamento: cursando
 por jamiel » Seg Mai 16, 2011 23:52
por jamiel » Seg Mai 16, 2011 23:52
Putz .. desculpa! Eu pus minha meia resolução, de prima. Mas é
![{9}^{x}=3*\sqrt[]{3} {9}^{x}=3*\sqrt[]{3}](/latexrender/pictures/977eab81c84c977b6829818b015f2f9d.png)
.
-
jamiel
- Colaborador Voluntário

-
- Mensagens: 131
- Registrado em: Seg Jan 31, 2011 15:48
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Mecânica
- Andamento: cursando
 por MarceloFantini » Ter Mai 17, 2011 00:10
por MarceloFantini » Ter Mai 17, 2011 00:10
Jamiel,
tome muito cuidado:
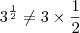
.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por Claudin » Ter Mai 17, 2011 17:43
por Claudin » Ter Mai 17, 2011 17:43
"O que sabemos é uma gota, o que não sabemos é um oceano." - Isaac Newton
-
Claudin
- Colaborador Voluntário

-
- Mensagens: 913
- Registrado em: Qui Mai 12, 2011 17:34
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
Voltar para Logaritmos
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Problema na resolução do logaritmo]
por Mayra Luna » Qui Out 25, 2012 20:14
- 2 Respostas
- 1509 Exibições
- Última mensagem por Mayra Luna

Qui Out 25, 2012 21:24
Logaritmos
-
- [Logaritmo] - Dúvida na resolução
por mota_16 » Dom Dez 08, 2013 19:43
- 3 Respostas
- 1841 Exibições
- Última mensagem por mota_16

Dom Dez 08, 2013 21:30
Logaritmos
-
- Resolução de equações com logaritmo
por Ana Saldanha » Sáb Mar 22, 2014 17:23
- 1 Respostas
- 1867 Exibições
- Última mensagem por DanielFerreira

Sáb Mar 22, 2014 19:24
Logaritmos
-
- [Logaritmo] duas questões para resolução com urgência
por Cristian Cristiano » Qua Mai 03, 2017 04:37
- 0 Respostas
- 4053 Exibições
- Última mensagem por Cristian Cristiano

Qua Mai 03, 2017 04:37
Logaritmos
-
- [Derivada de Logaritmo Natural] Exercício de logaritmo
por Ronaldobb » Dom Out 28, 2012 17:40
- 1 Respostas
- 2571 Exibições
- Última mensagem por MarceloFantini

Dom Out 28, 2012 18:16
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
cálculo de limites
Autor:
Hansegon - Seg Ago 25, 2008 11:29
Bom dia.
Preciso de ajuda na solução deste problema, pois só chego ao resultado de 0 sobre 0.
Obrigado
\lim_{x\rightarrow-1} x³ +1/x²-1[/tex]
Assunto:
cálculo de limites
Autor:
Molina - Seg Ago 25, 2008 13:25

Realmente se você jogar o -1 na equação dá 0 sobre 0.
Indeterminações deste tipo você pode resolver por L'Hôpital
que utiliza derivada.
Outro modo é transformar o numerador e/ou denominador
para que não continue dando indeterminado.
Dica: dividir o numerador e o denominador por algum valor é uma forma que normalmente dá certo.

Caso ainda não tenha dado uma

, avisa que eu resolvo.
Bom estudo!
Assunto:
cálculo de limites
Autor:
Guill - Dom Abr 08, 2012 16:03



Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![log{}_{2}\sqrt[5]{4}
{2}^{x}={2}^{\frac{2}{5}}
x = 2/5 log{}_{2}\sqrt[5]{4}
{2}^{x}={2}^{\frac{2}{5}}
x = 2/5](/latexrender/pictures/b083ee437c169c3507337ac6440f1979.png)
![log{}_{9}3\sqrt[]{3}
{3}^{2x}=3\sqrt[]{3},
{3}^{2x}=\sqrt[]{{3}^{3}3} log{}_{9}3\sqrt[]{3}
{3}^{2x}=3\sqrt[]{3},
{3}^{2x}=\sqrt[]{{3}^{3}3}](/latexrender/pictures/0e4f5187276dd4015379a89aeeb26045.png)

![log{}_{2}\sqrt[5]{4}
{2}^{x}={2}^{\frac{2}{5}}
x = 2/5 log{}_{2}\sqrt[5]{4}
{2}^{x}={2}^{\frac{2}{5}}
x = 2/5](/latexrender/pictures/b083ee437c169c3507337ac6440f1979.png)
![log{}_{9}3\sqrt[]{3}
{3}^{2x}=3\sqrt[]{3},
{3}^{2x}=\sqrt[]{{3}^{3}3} log{}_{9}3\sqrt[]{3}
{3}^{2x}=3\sqrt[]{3},
{3}^{2x}=\sqrt[]{{3}^{3}3}](/latexrender/pictures/0e4f5187276dd4015379a89aeeb26045.png)








![{9}^{x}=3*\sqrt[]{3} {9}^{x}=3*\sqrt[]{3}](/latexrender/pictures/977eab81c84c977b6829818b015f2f9d.png) .
.

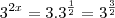



![9^x = 3\sqrt[2]{3} 9^x = 3\sqrt[2]{3}](/latexrender/pictures/ff4f8cf466660e6469898a30f338453f.png)








 , avisa que eu resolvo.
, avisa que eu resolvo.

