 por AlbertoAM » Sáb Mai 14, 2011 21:36
por AlbertoAM » Sáb Mai 14, 2011 21:36
O desenho seguinte representa uma plataforma petrolífera submarina P, situada a
![4 \,\sqrt[]{2} 4 \,\sqrt[]{2}](/latexrender/pictures/792215aec08dfddb9138ce12b7e7a8a0.png)
km da linha da praia e uma estação de refino R distante 10 km da projeção ortogonal P' de P.Deseja-se conectar, através de tubulações, a plataforma P com a estação R.Sabendo que o custo da tubulação submersa é o triplo do custo da tubulação terrestre, determinar a posição do entroncamento E na linha da praia, demodo que o custo seja mínimo.R.:
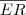
=8km
Pessoal to meio perdido nesse exercício aqui, não estou conseguindo montar a função a ser otimizada, poderiam me ajudar por favor.
-
AlbertoAM
- Usuário Dedicado

-
- Mensagens: 41
- Registrado em: Qui Nov 11, 2010 15:33
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: cursando
 por LuizAquino » Dom Mai 15, 2011 14:29
por LuizAquino » Dom Mai 15, 2011 14:29
A figura abaixo ilustra com mais detalhe o exercício.
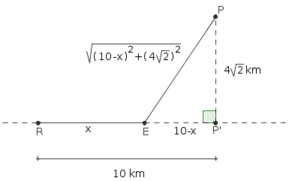
- exercicio-otimizacao.png (13.92 KiB) Exibido 2461 vezes
Agora, basta perceber que se o custo por km da tubulação terrestre for de 1 unidade monetária, então o custo por km da tubulação submersa será de 3 unidades monetárias.
Desse modo, o custo total será

.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por AlbertoAM » Dom Mai 15, 2011 16:22
por AlbertoAM » Dom Mai 15, 2011 16:22
Com você explicando pareceu banal a resolução, mas quando eu estava tentando resolver sozinho nem imaginava que era isso.Eu só não entendi porque no enunciado ele disse que o custo da tubulação submersa é o triplo do custo da tubulação terrestre e no desenho a tubulação submersa que é

, que se localiza acima da linha da praia, e não abaixo dela, isso me confundiu.
Muito obrigado Luiz Aquino.
-
AlbertoAM
- Usuário Dedicado

-
- Mensagens: 41
- Registrado em: Qui Nov 11, 2010 15:33
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: cursando
 por AlbertoAM » Dom Mai 15, 2011 19:23
por AlbertoAM » Dom Mai 15, 2011 19:23
Compreendi agora.Como sempre muito atencioso.
Obrigado.
-
AlbertoAM
- Usuário Dedicado

-
- Mensagens: 41
- Registrado em: Qui Nov 11, 2010 15:33
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Otimizacao
por Taisa » Sex Nov 12, 2010 13:53
- 1 Respostas
- 2143 Exibições
- Última mensagem por MarceloFantini

Sex Nov 12, 2010 14:36
Cálculo: Limites, Derivadas e Integrais
-
- Otimização
por elbert005 » Ter Mai 31, 2011 15:41
- 4 Respostas
- 3620 Exibições
- Última mensagem por LuizAquino

Ter Mai 31, 2011 18:08
Cálculo: Limites, Derivadas e Integrais
-
- Otimizacao !!!!!!
 por andersoneng » Qua Jun 27, 2012 12:26
por andersoneng » Qua Jun 27, 2012 12:26
- 7 Respostas
- 5270 Exibições
- Última mensagem por andersoneng

Qui Jun 28, 2012 10:24
Cálculo: Limites, Derivadas e Integrais
-
- Otimização
por Jhonata » Seg Fev 25, 2013 19:24
- 1 Respostas
- 1408 Exibições
- Última mensagem por Russman

Seg Fev 25, 2013 20:28
Cálculo: Limites, Derivadas e Integrais
-
- oTIMIZAÇÃO
por Pinheiro Rosa Victor » Qui Mai 02, 2013 11:11
- 0 Respostas
- 1253 Exibições
- Última mensagem por Pinheiro Rosa Victor

Qui Mai 02, 2013 11:11
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 4 visitantes
Assunto:
(FGV) ... função novamente rs
Autor:
my2009 - Qua Dez 08, 2010 21:48
Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
Assunto:
(FGV) ... função novamente rs
Autor: Anonymous - Qui Dez 09, 2010 17:25
Uma função de 1º grau é dada por

.
Temos que para

,

e para

,

.

Ache o valor de

e

, monte a função e substitua

por

.
Assunto:
(FGV) ... função novamente rs
Autor:
Pinho - Qui Dez 16, 2010 13:57
my2009 escreveu:Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
f(x)= 2.x
f(3)=2.3=6
f(4)=2.4=8
f(10)=2.10=20
Assunto:
(FGV) ... função novamente rs
Autor:
dagoth - Sex Dez 17, 2010 11:55
isso ai foi uma questao da FGV?
haahua to precisando trocar de faculdade.
Assunto:
(FGV) ... função novamente rs
Autor:
Thiago 86 - Qua Mar 06, 2013 23:11
Saudações!

ví suaquestão e tentei resolver, depois você conta-me se eu acertei.
Uma função de 1º grau é dada por y=3a+b
Resposta :
3a+b=6 x(4)
4a+b=8 x(-3)
12a+4b=24
-12a-3b=-24
b=0
substituindo b na 1°, ttenho que: 3a+b=6
3a+0=6
a=2
substituindo em: y=3a+b
y=30+0
y=30

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![4 \,\sqrt[]{2} 4 \,\sqrt[]{2}](/latexrender/pictures/792215aec08dfddb9138ce12b7e7a8a0.png) km da linha da praia e uma estação de refino R distante 10 km da projeção ortogonal P' de P.Deseja-se conectar, através de tubulações, a plataforma P com a estação R.Sabendo que o custo da tubulação submersa é o triplo do custo da tubulação terrestre, determinar a posição do entroncamento E na linha da praia, demodo que o custo seja mínimo.R.:
km da linha da praia e uma estação de refino R distante 10 km da projeção ortogonal P' de P.Deseja-se conectar, através de tubulações, a plataforma P com a estação R.Sabendo que o custo da tubulação submersa é o triplo do custo da tubulação terrestre, determinar a posição do entroncamento E na linha da praia, demodo que o custo seja mínimo.R.: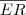 =8km
=8km

 .
.
 , que se localiza acima da linha da praia, e não abaixo dela, isso me confundiu.
, que se localiza acima da linha da praia, e não abaixo dela, isso me confundiu. .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.
