![4 \,\sqrt[]{2} 4 \,\sqrt[]{2}](/latexrender/pictures/792215aec08dfddb9138ce12b7e7a8a0.png) km da linha da praia e uma estação de refino R distante 10 km da projeção ortogonal P' de P.Deseja-se conectar, através de tubulações, a plataforma P com a estação R.Sabendo que o custo da tubulação submersa é o triplo do custo da tubulação terrestre, determinar a posição do entroncamento E na linha da praia, demodo que o custo seja mínimo.R.:
km da linha da praia e uma estação de refino R distante 10 km da projeção ortogonal P' de P.Deseja-se conectar, através de tubulações, a plataforma P com a estação R.Sabendo que o custo da tubulação submersa é o triplo do custo da tubulação terrestre, determinar a posição do entroncamento E na linha da praia, demodo que o custo seja mínimo.R.: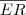 =8km
=8kmPessoal to meio perdido nesse exercício aqui, não estou conseguindo montar a função a ser otimizada, poderiam me ajudar por favor.


 .
.
 , que se localiza acima da linha da praia, e não abaixo dela, isso me confundiu.
, que se localiza acima da linha da praia, e não abaixo dela, isso me confundiu.![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
 e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)