Lorraine...
Note que a função modular tem uma característica específica... o módulo jamais é menor que zero... (isso não quer dizer que a função não tenha imagem negativa)
Assim, pra facilitar nossa vida, podemos reescrever a função, retirando-a do módulo... e teremos duas funções distintas condicionadas ao valor de x, para garantir que o resultado do módulo seja positivo...
Essas duas funções nos darão linhas diferentes, que teremos que combinar em suas áreas válidadas (onde o módulo é

e teremos o gráfico da função...
Para encontrar o vértice e a imagem positiva, não é necessário fazer o gráfico, mas, como o exercício pede, vc terá que fazer... rs
vamos, então, extrair as funções condicionadas:
g(x)=|x+4|...
Sabemos que se g(x)<0, então |g(x)| = -g(x)... certo?
Então,
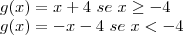
O vértice é o ponto onde o módulo é zero...
|x+4|=0
x=-4...
Nesse caso,

...
Escolha um valor de x<-4 e outro x>-4 e vc poderá traçar as duas retas
Para a outra, realize os mesmos passos... contudo, note 2-3|x+4| te dará valores negativos sempre que 3|x+4|>2
Faz o gráfico... se ficar com dúvida, posta...
Um abraço
 e f(x)=2-3
e f(x)=2-3
 e onde f(x)
e onde f(x)

 e f(x)=2-3
e f(x)=2-3
 e onde f(x)
e onde f(x)


 e teremos o gráfico da função...
e teremos o gráfico da função...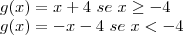
 ...
...


 .
.
 :
: