 por maria cleide » Qui Mai 12, 2011 17:58
por maria cleide » Qui Mai 12, 2011 17:58
Na figura, ABCDE e F são vértices de um hexágono regular inscrito num círculo, cujo raio mede 1m. A área da região hachurada é quanto em
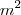
?
Supus que a área hachurada era um terço, pois cada a cirgunferência foi dividida em 3 partes diferentes, logo encontrei a área do hexagono formado pela união dos triângulos e dividi por 3:
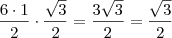
. Mas foi somente uma suposiçao, como fazer?
- Anexos
-
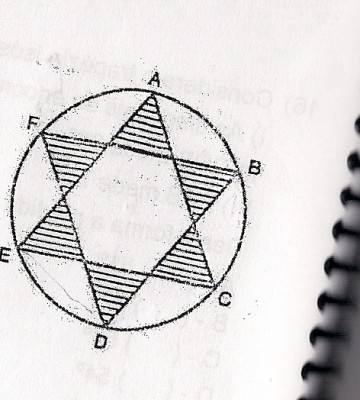
-
maria cleide
- Usuário Parceiro

-
- Mensagens: 54
- Registrado em: Dom Mai 08, 2011 12:57
- Formação Escolar: ENSINO FUNDAMENTAL I
- Andamento: cursando
 por MarceloFantini » Qui Mai 12, 2011 18:37
por MarceloFantini » Qui Mai 12, 2011 18:37
Você não pode supor que a área hachurada é um terço.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por maria cleide » Qui Mai 12, 2011 20:42
por maria cleide » Qui Mai 12, 2011 20:42
Mas então, como posso desenvolver o problema?
-
maria cleide
- Usuário Parceiro

-
- Mensagens: 54
- Registrado em: Dom Mai 08, 2011 12:57
- Formação Escolar: ENSINO FUNDAMENTAL I
- Andamento: cursando
 por FilipeCaceres » Qui Mai 12, 2011 21:08
por FilipeCaceres » Qui Mai 12, 2011 21:08
Ola Maria Cleide,
Só uma coisinha, como se trata de uma apostila acredito de deva ter os gabaritos, sendo assim peço que sempre os tiver peço que poste juntamente.
Como se trata de um hexagono,observe que este estralhado hachurada nada mais é do que dois triângulos equiláteros, sendo que um rotacionado.
A área de um triângulo equilátero é fácil
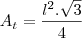
, agora observe que temos um "furo" na intersecção dos dois triângulos com um formato de hexagono(
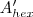
) também.
Logo, para saber o valor do restante, basta fazer:
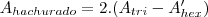
Qualquer dúvida poste novamente.
-
FilipeCaceres
- Colaborador Voluntário

-
- Mensagens: 351
- Registrado em: Dom Out 31, 2010 21:43
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Tec. Mecatrônica
- Andamento: formado
 por FilipeCaceres » Qui Mai 12, 2011 21:39
por FilipeCaceres » Qui Mai 12, 2011 21:39
Uma outra forma mais simples seria fazer o seguinte, calcular qual é a altura dos "triângulozinhos" que vale
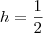
e como sabemos que um hexagono é formado por 6 triângulos equiláteros, bastava você calcular qual seria a altura deles, e desta forma você decobriria que ambos tem a mesma medida, portanto a área hachurada é igual a área do hexagono menor.
Agora só resta vc achar quando vale o lado deste hexagono menor e calcular sua área.
Abraço.
-
FilipeCaceres
- Colaborador Voluntário

-
- Mensagens: 351
- Registrado em: Dom Out 31, 2010 21:43
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Tec. Mecatrônica
- Andamento: formado
 por maria cleide » Qui Mai 12, 2011 23:01
por maria cleide » Qui Mai 12, 2011 23:01
Meu problema é como achar o lado do triângulo, como posso encontra-lo?
-
maria cleide
- Usuário Parceiro

-
- Mensagens: 54
- Registrado em: Dom Mai 08, 2011 12:57
- Formação Escolar: ENSINO FUNDAMENTAL I
- Andamento: cursando
 por FilipeCaceres » Sex Mai 13, 2011 01:02
por FilipeCaceres » Sex Mai 13, 2011 01:02
Basta você saber que quando temos um triângulo equilátero inscrito em uma circunferênria temos as seguintes relações:
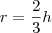
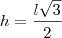
Qualquer dúvida poste novamente.
Abraço.
-
FilipeCaceres
- Colaborador Voluntário

-
- Mensagens: 351
- Registrado em: Dom Out 31, 2010 21:43
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Tec. Mecatrônica
- Andamento: formado
 por maria cleide » Sex Mai 13, 2011 22:15
por maria cleide » Sex Mai 13, 2011 22:15
Solução: Como a altura do triângulo menor é

a do maior é

. Descobri o valor do lado do triângulo equilátero maior com base na igualdade
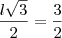
encontrando
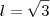
, logo o lado do triângulo menor que é a mesma do hexagono será

. Então calculei o valor da área do hexagono
![\dfrac{6\cdot\dfrac{\sqrt{3}}{3}}{2}}\cdot\dfrac{\sqrt{3}}{2}=[tex]\dfrac{3}{2} \dfrac{6\cdot\dfrac{\sqrt{3}}{3}}{2}}\cdot\dfrac{\sqrt{3}}{2}=[tex]\dfrac{3}{2}](/latexrender/pictures/933e9734caee893e0ce1b480c4ea844d.png)
[/tex]. Porém o resultado não bateu com o gabarito que mostra que o valor é
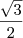
. Você consegue identificar onde errei?
-
maria cleide
- Usuário Parceiro

-
- Mensagens: 54
- Registrado em: Dom Mai 08, 2011 12:57
- Formação Escolar: ENSINO FUNDAMENTAL I
- Andamento: cursando
 por FilipeCaceres » Sex Mai 13, 2011 22:28
por FilipeCaceres » Sex Mai 13, 2011 22:28
A área do hexágono é igual a seis vezes a área de um triângulo equilátero, logo

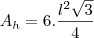
Como o lado vale,
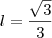
Assim temos,
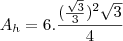
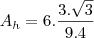
Portanto,
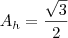
Abraço.
-
FilipeCaceres
- Colaborador Voluntário

-
- Mensagens: 351
- Registrado em: Dom Out 31, 2010 21:43
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Tec. Mecatrônica
- Andamento: formado
 por maria cleide » Sex Mai 13, 2011 22:41
por maria cleide » Sex Mai 13, 2011 22:41
Obrigada! Até breve.
Abraço Maria Cleide.
-
maria cleide
- Usuário Parceiro

-
- Mensagens: 54
- Registrado em: Dom Mai 08, 2011 12:57
- Formação Escolar: ENSINO FUNDAMENTAL I
- Andamento: cursando
Voltar para Geometria Plana
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
Usuários navegando neste fórum: Nenhum usuário registrado e 3 visitantes
Assunto:
(FGV) ... função novamente rs
Autor:
my2009 - Qua Dez 08, 2010 21:48
Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
Assunto:
(FGV) ... função novamente rs
Autor: Anonymous - Qui Dez 09, 2010 17:25
Uma função de 1º grau é dada por

.
Temos que para

,

e para

,

.

Ache o valor de

e

, monte a função e substitua

por

.
Assunto:
(FGV) ... função novamente rs
Autor:
Pinho - Qui Dez 16, 2010 13:57
my2009 escreveu:Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
f(x)= 2.x
f(3)=2.3=6
f(4)=2.4=8
f(10)=2.10=20
Assunto:
(FGV) ... função novamente rs
Autor:
dagoth - Sex Dez 17, 2010 11:55
isso ai foi uma questao da FGV?
haahua to precisando trocar de faculdade.
Assunto:
(FGV) ... função novamente rs
Autor:
Thiago 86 - Qua Mar 06, 2013 23:11
Saudações!

ví suaquestão e tentei resolver, depois você conta-me se eu acertei.
Uma função de 1º grau é dada por y=3a+b
Resposta :
3a+b=6 x(4)
4a+b=8 x(-3)
12a+4b=24
-12a-3b=-24
b=0
substituindo b na 1°, ttenho que: 3a+b=6
3a+0=6
a=2
substituindo em: y=3a+b
y=30+0
y=30

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
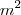 ?
?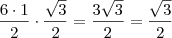 . Mas foi somente uma suposiçao, como fazer?
. Mas foi somente uma suposiçao, como fazer?
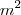 ?
?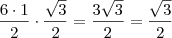 . Mas foi somente uma suposiçao, como fazer?
. Mas foi somente uma suposiçao, como fazer?


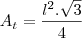 , agora observe que temos um "furo" na intersecção dos dois triângulos com um formato de hexagono(
, agora observe que temos um "furo" na intersecção dos dois triângulos com um formato de hexagono(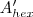 ) também.
) também.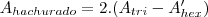

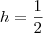 e como sabemos que um hexagono é formado por 6 triângulos equiláteros, bastava você calcular qual seria a altura deles, e desta forma você decobriria que ambos tem a mesma medida, portanto a área hachurada é igual a área do hexagono menor.
e como sabemos que um hexagono é formado por 6 triângulos equiláteros, bastava você calcular qual seria a altura deles, e desta forma você decobriria que ambos tem a mesma medida, portanto a área hachurada é igual a área do hexagono menor.

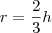
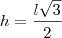

 a do maior é
a do maior é  . Descobri o valor do lado do triângulo equilátero maior com base na igualdade
. Descobri o valor do lado do triângulo equilátero maior com base na igualdade 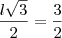 encontrando
encontrando 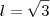 , logo o lado do triângulo menor que é a mesma do hexagono será
, logo o lado do triângulo menor que é a mesma do hexagono será  . Então calculei o valor da área do hexagono
. Então calculei o valor da área do hexagono ![\dfrac{6\cdot\dfrac{\sqrt{3}}{3}}{2}}\cdot\dfrac{\sqrt{3}}{2}=[tex]\dfrac{3}{2} \dfrac{6\cdot\dfrac{\sqrt{3}}{3}}{2}}\cdot\dfrac{\sqrt{3}}{2}=[tex]\dfrac{3}{2}](/latexrender/pictures/933e9734caee893e0ce1b480c4ea844d.png) [/tex]. Porém o resultado não bateu com o gabarito que mostra que o valor é
[/tex]. Porém o resultado não bateu com o gabarito que mostra que o valor é 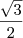 . Você consegue identificar onde errei?
. Você consegue identificar onde errei?

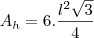
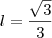
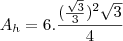
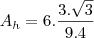
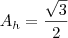


 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.
