 . Assinale a alternativa falsa:
. Assinale a alternativa falsa:
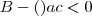
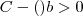


Eu fiz eliminando as falsas de acordo com a relação :
 e encontrei
e encontrei  (letra C). Existe outras relações que podem me ajudar na resoluçao deste problema?
(letra C). Existe outras relações que podem me ajudar na resoluçao deste problema?
 . Assinale a alternativa falsa:
. Assinale a alternativa falsa:
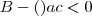
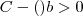


 e encontrei
e encontrei  (letra C). Existe outras relações que podem me ajudar na resoluçao deste problema?
(letra C). Existe outras relações que podem me ajudar na resoluçao deste problema?
 , pois sabemos que esse é o valor de
, pois sabemos que esse é o valor de  e que, como a parábola cruza o eixo x em dois pontos distintos, então
e que, como a parábola cruza o eixo x em dois pontos distintos, então  é verdadeira...
é verdadeira...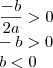

Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante


 , avisa que eu resolvo.
, avisa que eu resolvo.

