 por maria cleide » Ter Mai 10, 2011 21:52
por maria cleide » Ter Mai 10, 2011 21:52
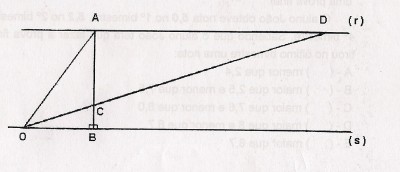
Na figura do anexo, as retas r e s são paralelas e o segmento

é perpendicular a elas.
Sabendo-se que
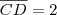
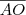
e que
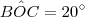
. Então o ângulo
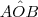
mede quanto?
Encontrei o valor dos ângulos:
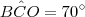

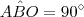
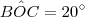
Mas agora não sei como continuar o problema.
- Anexos
-
-
maria cleide
- Usuário Parceiro

-
- Mensagens: 54
- Registrado em: Dom Mai 08, 2011 12:57
- Formação Escolar: ENSINO FUNDAMENTAL I
- Andamento: cursando
 por FilipeCaceres » Ter Mai 10, 2011 22:10
por FilipeCaceres » Ter Mai 10, 2011 22:10
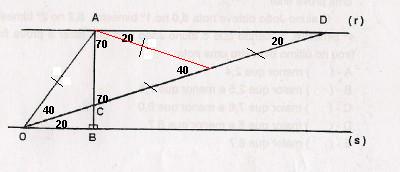
- digitalizar.JPG (9.39 KiB) Exibido 902 vezes
Criei um reta auxiliar (vermelho) dividindo CD em duas partes iguais (mediana), agora observe que temos vários triângulos isósceles, com isso é fácil perceber que
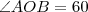
Eu já resolvi na própria figura caso não entenda poste sua dúvida.
Abraço
-
FilipeCaceres
- Colaborador Voluntário

-
- Mensagens: 351
- Registrado em: Dom Out 31, 2010 21:43
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Tec. Mecatrônica
- Andamento: formado
Voltar para Geometria Plana
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Ângulo/circunferência] Ângulo CÂB, ajude-me!
 por miltonsermoud » Qua Set 30, 2015 17:14
por miltonsermoud » Qua Set 30, 2015 17:14
- 3 Respostas
- 3508 Exibições
- Última mensagem por miltonsermoud

Sex Out 02, 2015 07:41
Geometria Plana
-
- medidas
por thayna » Sáb Out 23, 2010 12:08
- 1 Respostas
- 2295 Exibições
- Última mensagem por VtinxD

Dom Out 24, 2010 00:38
Geometria Plana
-
- Medidas
por Walquiria » Dom Nov 06, 2011 19:30
- 2 Respostas
- 1977 Exibições
- Última mensagem por Walquiria

Seg Nov 07, 2011 19:03
Estatística
-
- medidas
 por ana celia » Qua Set 12, 2012 17:57
por ana celia » Qua Set 12, 2012 17:57
- 5 Respostas
- 3095 Exibições
- Última mensagem por Cleyson007

Qui Set 13, 2012 10:47
Geometria Plana
-
- Conversão de medidas
por eduardopiana » Ter Out 21, 2008 14:48
- 6 Respostas
- 7450 Exibições
- Última mensagem por Giles

Qua Out 29, 2008 23:40
Conversão de Unidades
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 é perpendicular a elas.
é perpendicular a elas.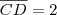
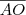 e que
e que 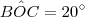 . Então o ângulo
. Então o ângulo 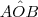 mede quanto?
mede quanto?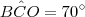

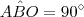
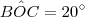

 é perpendicular a elas.
é perpendicular a elas.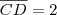
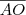 e que
e que 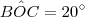 . Então o ângulo
. Então o ângulo 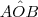 mede quanto?
mede quanto?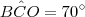

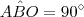
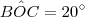

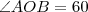


 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , mas negativo pois tem de ser no quarto quadrante. Se
, mas negativo pois tem de ser no quarto quadrante. Se  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.