 por andersontricordiano » Qui Mai 05, 2011 20:19
por andersontricordiano » Qui Mai 05, 2011 20:19
CALCULE O CALCULO DA FUNÇÃO QUE CONTEM LOGARITMO :
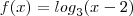
DADOS OS VALORES PARA x :
a)Se x=-2
b)Se x=-1
c)Se x=1
d)Se x=0
Detalhe as resposta são:a)=

b)=

c)=

d)=
 Agradeço muito quem resolver esse calculo
Agradeço muito quem resolver esse calculoEditado pela última vez por
andersontricordiano em Sex Mai 06, 2011 02:50, em um total de 2 vezes.
-
andersontricordiano
- Colaborador Voluntário

-
- Mensagens: 192
- Registrado em: Sex Mar 04, 2011 23:02
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por MarceloFantini » Sex Mai 06, 2011 00:11
por MarceloFantini » Sex Mai 06, 2011 00:11
Tem certeza que não se confundiu? A função não existe para estes valores.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por andersontricordiano » Sex Mai 06, 2011 02:33
por andersontricordiano » Sex Mai 06, 2011 02:33
ok!
A resposta da letra d eu tinha colocado outro valor errado.Que tem como resultado 3.
Mas as outras alternativa estão como está no gabarito do livro
-
andersontricordiano
- Colaborador Voluntário

-
- Mensagens: 192
- Registrado em: Sex Mar 04, 2011 23:02
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por Molina » Sex Mai 06, 2011 13:00
por Molina » Sex Mai 06, 2011 13:00
Bom dia, Anderson.
O que o Fantini quis dizer é que o logaritmando precisa ser maior do que zero, para a função existir.
Por exemplo, não tem sentido perguntar qual o

, pois 3 elevado a nenhum número vai ter como resultado -2.
No seu outro tópico (que eu exclui, por sinal) você havia colocado

... Coloque a questão como está no livro ou então tire uma foto dela e coloque aqui.
Ficamos no aguardo!
Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por andersontricordiano » Sex Mai 06, 2011 16:38
por andersontricordiano » Sex Mai 06, 2011 16:38
Ok está escrita no livro.
Seja


definida por

e
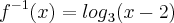
Represente

no mesmo plano.
DADOS OS VALORES PARA x :
a)Se x=-2
b)Se x=-1
c)Se x=1
d)Se x=0
é assim que está eu também estou achando estranho a resposta! pois
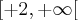
-
andersontricordiano
- Colaborador Voluntário

-
- Mensagens: 192
- Registrado em: Sex Mar 04, 2011 23:02
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
Voltar para Funções
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Calcule em função o logaritmo.
por andersontricordiano » Sáb Abr 02, 2011 17:54
- 1 Respostas
- 1720 Exibições
- Última mensagem por Elcioschin

Sáb Abr 02, 2011 23:27
Logaritmos
-
- Calcule a raiz da função do 1º grau?
por breno1323 » Ter Jun 05, 2012 11:44
- 3 Respostas
- 1764 Exibições
- Última mensagem por joaofonseca

Ter Jun 05, 2012 12:30
Funções
-
- Calcule em função de a e b os seguintes logaritmos decimais
por andersontricordiano » Qui Mar 24, 2011 16:55
- 3 Respostas
- 4425 Exibições
- Última mensagem por profmatematica

Sex Mar 25, 2011 12:17
Logaritmos
-
- Calcule em função de a e b os seguintes logaritmos decimais
por andersontricordiano » Qui Mar 24, 2011 16:57
- 1 Respostas
- 1429 Exibições
- Última mensagem por LuizAquino

Qui Mar 24, 2011 17:23
Logaritmos
-
- Logaritmo em função de n
por Lana Brasil » Seg Jul 21, 2014 22:06
- 2 Respostas
- 2033 Exibições
- Última mensagem por Pessoa Estranha

Ter Jul 22, 2014 00:32
Logaritmos
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
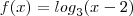





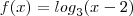








 , pois 3 elevado a nenhum número vai ter como resultado -2.
, pois 3 elevado a nenhum número vai ter como resultado -2. ... Coloque a questão como está no livro ou então tire uma foto dela e coloque aqui.
... Coloque a questão como está no livro ou então tire uma foto dela e coloque aqui.

 definida por
definida por  e
e 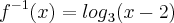
 no mesmo plano.
no mesmo plano.

 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , mas negativo pois tem de ser no quarto quadrante. Se
, mas negativo pois tem de ser no quarto quadrante. Se  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.