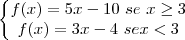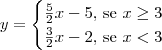Rs... é mais ou menos por aí...
A questão da função modular é que ela não aceita valores negativos na imagem, mas o domínio aceita qualquer valor. Assim, podemos escrever a função de formas diferentes para ilustrá-la melhor.
O comportamento dela vai depender de seu grau. Como podemos ver pelos exemplos utilizados, a função modular de 1º grau apresenta gráfico em V, a de 2º forma um W, a de 3º (essa não temos aqui) formará duas curvas que partem do ponto y=0, mas que não apresentam qualquer simetria, ou seja, a função modular não é necessariamente simétrica. Sua característica principal é que o ponto (ou pontos) y=0 divide a função em segmentos, que podem ser definidos por funções condicionais.
Explicando melhor, se f(x) < 0 para um x qualquer, então |f(x)| = - f(x)
Foi falha minha, mas o gráfico da segunda função fica assim:
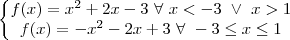
Traduzindo,
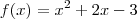
para todo x menor que -3 ou x maior que 1 (pois esses valores de x retornam y positivo) e
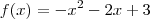
para todo x de -3 a 1 (pois esses valores de x retornam y negativo, sendo necessário inverter o sinal da função)...
Obviamente, existem funções que não apresentam imagem negativa... nestes casos, o módulo dessas funções não fará a mínima diferença... rs
Então, resumidamente, para traçar o gráfico de uma função modular, precisamos encontrar o domínio e a imagem da função contida dentro do módulo e verificar qual intervalo de D-->Im onde y>=0 e inverter o sinal da função para valores de x fora desse intervalo, traçamos e combinamos os gráfifcos das duas funções para encontrar o gráfico da função modular.
Espero ter ajudado... se surgiu mais alguma dúvida, pode perguntar, que estamos aqui pra isso... rs
Um abraço



 , então, podemos representá-la da seguinte forma:
, então, podemos representá-la da seguinte forma: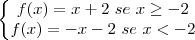
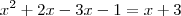 , logo:
, logo: 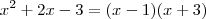
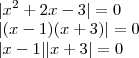
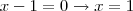 e
e 


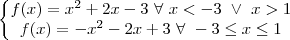
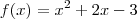 para todo x menor que -3 ou x maior que 1 (pois esses valores de x retornam y positivo) e
para todo x menor que -3 ou x maior que 1 (pois esses valores de x retornam y positivo) e 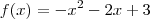 para todo x de -3 a 1 (pois esses valores de x retornam y negativo, sendo necessário inverter o sinal da função)...
para todo x de -3 a 1 (pois esses valores de x retornam y negativo, sendo necessário inverter o sinal da função)...